6.3 Nevezetes folytonos eloszlások

A diszkrét eloszlásokhoz hasonlóan a folytonos eloszlások közül is vannak olyanok, melyek valamilyen tulajdonságuk miatt gyakrabban alkalmazhatóak. Ezen eloszlások esetén jellemzően a sűrűség- és az eloszlásfüggvény is ismert, a szükséges paraméterek megadásával az eloszlás jól kezelhetővé válik. A sűrűségfüggvény alapján megtörténhet az eloszlás ábrázolása, ami segít elképzelni a valószínűség sűrűsödését, azonban a sűrűségfüggvény csak korlátozottan alkalmas valószínűségek számítására, a görbe alatti terület gyakran nehezen számítható. Az eloszlásfüggvény ebben segít, gyakorlatilag tetszőleges \(x\) értékhez megadva az adott értékhez tartozó baloldali görbe alatti területet.

A nevezetes eloszlások alkalmazása a valószínűségek könnyebb számíthatósága mellett azért is előnyös, mert a momentumok is a paraméterektől függő zárt képlettel rendelkeznek, azaz nem kell a (6.4) és (6.5) általános képleteket és integrálást alkalmazni, hanem egyszerűbb speciálisan az adott eloszlásra jellemző képletek állnak rendelkezésünkre.

Az alábbiakban a legegyszerűbb folytonos eloszlásokat mutatjuk be röviden, a további tanulmányok során ezeket még több folytonos eloszlás fogja követni. Az első két eloszlás jelentőségét az egyszerűségük adja, ennek ellenére fontos, gyakorlatban alkalmazható eloszlások, a normális eloszlás pedig a statisztika számára az egyik legfontosabb eloszlás.

6.3.1 Folytonos egyenletes eloszlás

Az egyenletes eloszlás az egyik legegyszerűbb folytonos eloszlás. Azt az esetet írja le, ha egy intervallumon valamennyi azonos hosszúságú részintervallum ugyanolyan valószínűséggel következik be, vagy más szavakkal, a valószínűség sűrűsödése egyenletes, azaz a sűrűségfüggvény konstans. A folytonos egyenletes eloszlásnak tehát két paramétere van, melyeket jelöljünk a diszkrét esethez hasonlóan \(a\)-val és \(b\)-vel, ahol \(a\) legkisebb, \(b\) pedig a legnagyobb lehetséges értéke \(X\)-nek.

Az \(X\sim\mathcal{U}(a,b)\) jelölést alkalmazva tehát a sűrűség- és eloszlásfüggvény:

\[\begin{equation} f(x)=\begin{cases} \frac{1}{b-a} &\text{ha}\ a \le x \le b, \\ 0 & \text{egyébként} \end{cases}\qquad F(x)= \begin{cases} 0 & \text{ha }x < a \\ \frac{x-a}{b-a} & \text{ha }a \le x < b \\ 1 & \text{ha }x \ge b \end{cases} \tag{6.7} \end{equation}\]

A folytonos egyenletes eloszlás momentumai a paraméterek segítségével könnyen megadhatók, azok hasonlítanak a (5.9) egyenletekben látottakhoz. A várható érték és a variancia a

\[\begin{equation} \mathbf{E}(X)=\dfrac{a+b}{2}, \qquad \mathbf{D}^2(X)=\dfrac{(b-a)^2}{12} \tag{6.8} \end{equation}\]

formulák segítségével számítható. Ha tudjuk, hogy a \(0-t\) időintervallumban pontosan 1 telefonhívás érkezik be, akkor joggal feltételezhetjük, hogy a telefonhívás ideje leírható az \(X\sim\mathcal{U}(0,t)\) eloszlással. Egyenletes eloszlással közelíthető egy szakaszra eső véletlenszerű pont helyzetének eloszlása, stb.

A fenti elméleti fejtegetéseket az alábbi példával szeretnénk érthetőbbé tenni. Tegyük fel, hogy egy telefonhívás érkezik be a következő 6 percen belül, jelölje \(X\) az eltelt időt és tételezzük fel, hogy \(X\sim\mathcal{U}(0,6)\). Ekkor

\[ f(x)=\begin{cases} \frac{1}{6} &\text{ha}\ 0 \le x \le 6, \\ 0 & \text{egyébként} \end{cases}\qquad F(x)= \begin{cases} 0 & \text{ha }x < 0 \\ \frac{x}{6} & \text{ha }0 \le x < 6 \\ 1 & \text{ha }x \ge 6 \end{cases} \]

Mivel \(X\) folytonos, ezért tudjuk, hogy \(\mathrm{P}(X=x) = 0\) minden \(x\)-re. A sűrűségfüggvény a 0-6 intervallumon konstans, könnyen ellenőrizhetjük azt is, hogy \(f(x)\) sűrűségfüggvény, hiszen \(f(x) \geq 0\) minden \(x\)-re, illetve a görbe alatti terület 1, hiszen egy olyan téglalapról van szó, melynek egyik oldala 6, a másik \(\frac{1}{6}\) hosszúságú.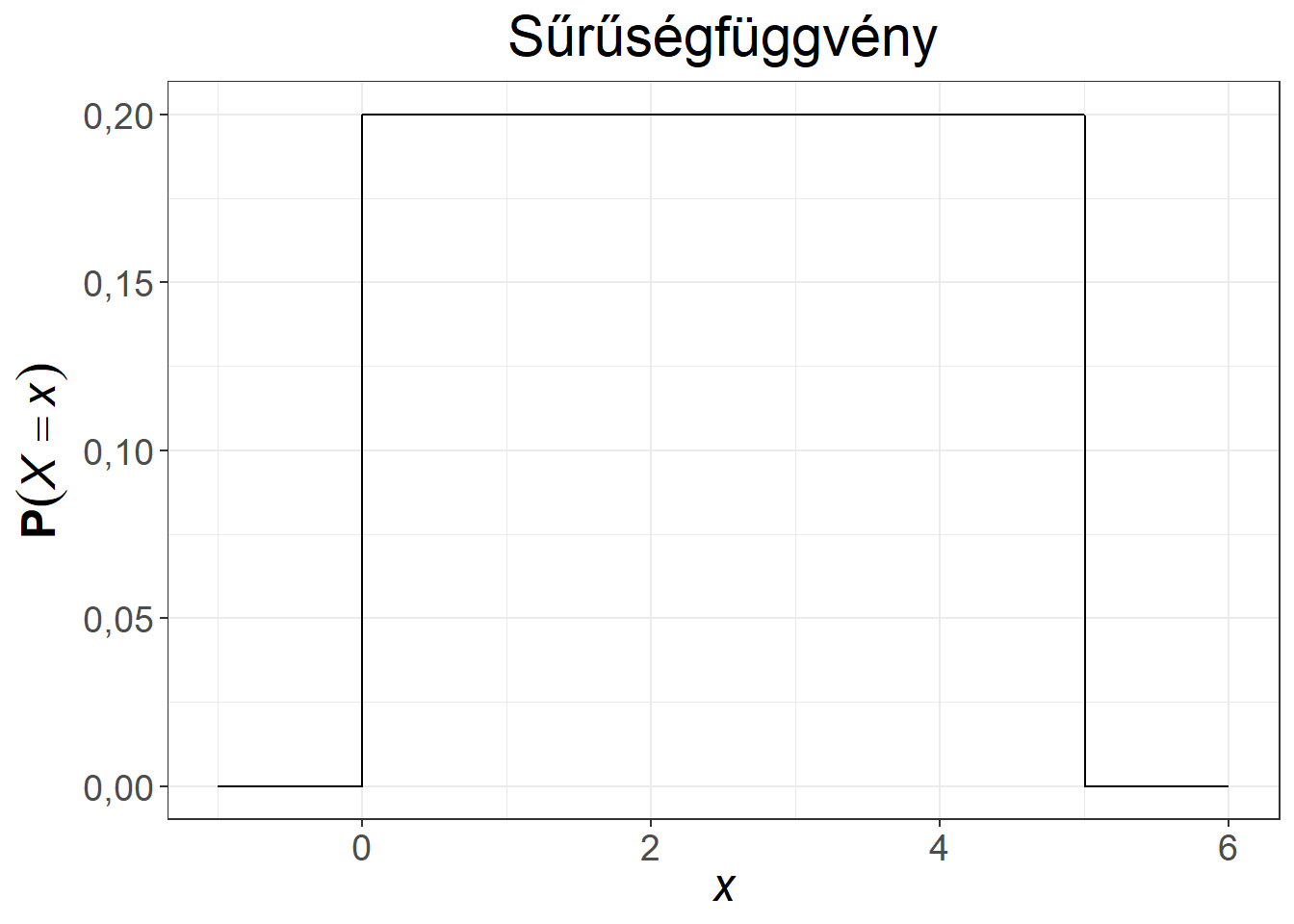

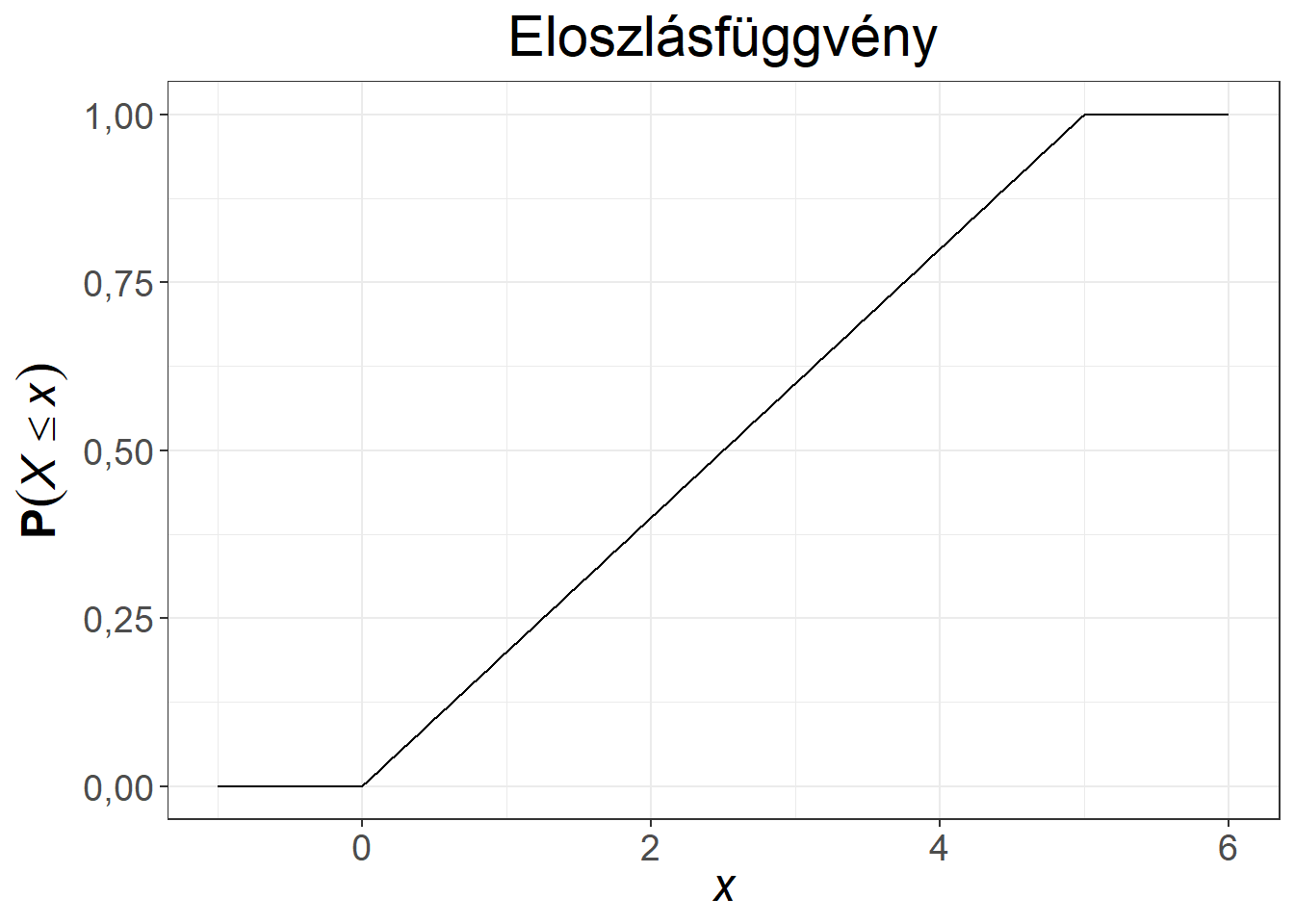
Ábra 6.3: Egyenletes eloszlású változó sűrűség- és eloszlásfüggvénye

Könnyen ellenőrizhető, hogy a sűrűségfüggvény \(-\infty\)-től \(x\)-ig vett integrálja épp az eloszlásfüggvény, illetve az eloszlásfüggvény deriváltja épp \(\dfrac{1}{6}\).

Példaként tekintsük annak az eseménynek a valószínűségét, hogy 3 percet, vagy annál kevesebbet kell várni a hívásra. A \(\mathbf{P} \left( X \leq 3\right)\) valószínűséget két módon is meghatározhatjuk, egyrészt a sűrűségfüggvényen az \(x = 3\) értéktől balra eső görbe alatti terület meghatározásával. A görbe alatti terület a \(\int_{-\infty}^3 \dfrac{1}{6} \mathrm{d} u\) kifejezés segítségével határozható meg, ami jelen esetben felesleges, hiszen egy téglalapról van szó, melynek egyik oldala 3, a másik \(\dfrac{1}{6}\) hosszúságú. A keresett valószínűség tehát a sűrűségfüggvény segítségével 0,5. Az eloszlásfüggvény segítségével sokkal könnyebb a keresett valószínűség meghatározása, hiszen csupán be kell helyettesítenünk az \(F(x)=\dfrac{x}{6}\) képletbe, amiből közvetlenül adódik, hogy a keresett valószínűség 0,5. Az eloszlásfüggvény ábrájáról ez a pont könnyedén leolvasható.

A fenti, baloldali valószínűség mellet a jobboldali valószínűségek, vagy az intervallumba esés valószínűsége is analóg módon számítható, akár a sűrűségfüggvény megfelelő integrálásával, vagy az eloszlásfüggvény alkalmazásával a fejezet elején felírt azonosságok alapján.

A momentumok segítségével a várható érték és a variancia könnyedén meghatározható, \(\mathbf{E}(X)=\dfrac{0+6}{2} = 3\), illetve \(\mathbf{D}^2(X)=\dfrac{36}{12} = 3\). Az általános (6.4) és (6.5) formulák alkalmazásával szintén megkaphattuk volna a momentumokat.

Kérdésként merülhet fel, hogy mi az az időtartam, ami esetén annak a valószínűsége, hogy maximum annyit kell várnunk épp 0,8. Most tehát egy valószínűséget ismerünk, méghozzá azt az \(x\) értéket keressük, amire teljesül, hogy \(\mathbf{P} \left( X \leq x\right) = 0{,}8\). Erre a kérdésre az eloszlásfüggvény inverze ad választ. Azt az \(x\)-et keressük tehát, amire \(F(x) = \frac{x}{6} = 0{,}8\), amiből egyszerűen kapjuk az \(x = 4{,}8\) megoldást. Tehát 0,8 valószínűséggel legfeljebb 4,8 percet kell várni a hívásra.

6.3.2 Exponenciális eloszlás

Az exponenciális eloszlást gyakran alkalmazzák véletlenszerű időtartamok leírására. Értelmezési tartománya a nemnegatív valós számok halmaza, egyetlen, pozitív paraméterrel rendelkezik, melyet \(\lambda\) jelöl. Az \(X\sim\text{Exp}(\lambda)\) jelölést alkalmazva tehát a sűrűség- és eloszlásfüggvény:

\[\begin{equation} f(x)=\begin{cases} \lambda \mathrm{e}^{-\lambda x}, &\text{ha } x \ge 0\\ 0 & \text{egyébként} \end{cases}\qquad F(x)= \begin{cases} 1-\mathrm{e}^{-\lambda x}, &\text{ha } x \ge 0\\ 0, & \text{egyébként} \end{cases} \tag{6.9} \end{equation}\]

A várható érték és a variancia a

\[\begin{equation} \mathbf{E}(X)=\dfrac{1}{\lambda}, \qquad \mathbf{D}^2(X)=\dfrac{1}{\lambda^2} \tag{6.10} \end{equation}\]

formulák segítségével számítható, tehát az exponenciális eloszlás esetén a várható érték megegyezik a szórással. Az exponenciális eloszlás egy fontos tulajdonsága, hogy "nincs memóriája", azaz belátható, hogy \(\mathbf{P} \left( X > x + s \vert X > s\right) = \mathbf{P} \left( X > x \right)\) minden nemnegatív \(x\) és \(s\) esetén. Azaz ha például egy meghibásodásig tartó időtartamot vizsgálunk, akkor ha a meghibásodás nem következett be az első \(x\) másodperc alatt, akkor annak a valószínűsége, hogy a meghibásodás nem következik be a következő \(s\) másodpercben pontosan ugyanannyi, mintha a 0 időponttól kezdve mérnénk az \(s\) másodpercet. Ez a tulajdonság nem mindig reális, ezért az exponenciális eloszlás egyéb változatait is gyakran alkalmazzák például meghibásodások vizsgálata esetén. A folytonos eloszlások közül egyedül az exponenciális eloszlás rendelkezik ezzel a tulajdonsággal.

Vizsgáljuk egy call-centerbe érkező hívások hosszát. Ha tudjuk, hogy a hívások átlagos hossza két perc, akkor gyakran alkalmazzuk a \(\lambda = 0{,}5\) exponenciális eloszlást (hiszen \(\mathbf{E}(X)=\dfrac{1}{\lambda} = 2\)).

Mi a valószínűsége, hogy a következő hívás 1 és 3 perc közötti időtartamot fog felölelni? Tudjuk, hogy \[ \mathbf{P} \left(1 < X <3 \right) = F(3) - F(1) = 1-\mathrm{e}^{-0{,}5 \cdot 3} - (1-\mathrm{e}^{-0{,}5}) = \mathrm{e}^{-0{,}5} - \mathrm{e}^{-1{,}5} = 0{,}3834 \]

A valószínűséget a sűrűségfüggvény 1-3 intervallumon vett integrálásával is megkaphattuk volna, ennek belátását az olvasóra bízzuk.

Mi az a híváshossz, amelynél a hívások 95%-a rövidebb? \[ \mathbf{P} \left(X < x \right) = F(x) = 1-\mathrm{e}^{-0{,}5 \cdot x} = 0{,}95 \] A fenti egyenletet rendezve azt kapjuk, hogy \[ \mathrm{e}^{-0{,}5 \cdot x} = 0{,}05 \] amiből \[ x = -\dfrac{\ln(0{,}05)}{0{,}5} = 5{,}991 \] percnél rövidebb a hívások 95%-a.

Az exponenciális eloszlás sűrűség- és eloszlásfüggvényét mutatja be a 6.4. ábra különböző \(\lambda\) paraméterek mellett.

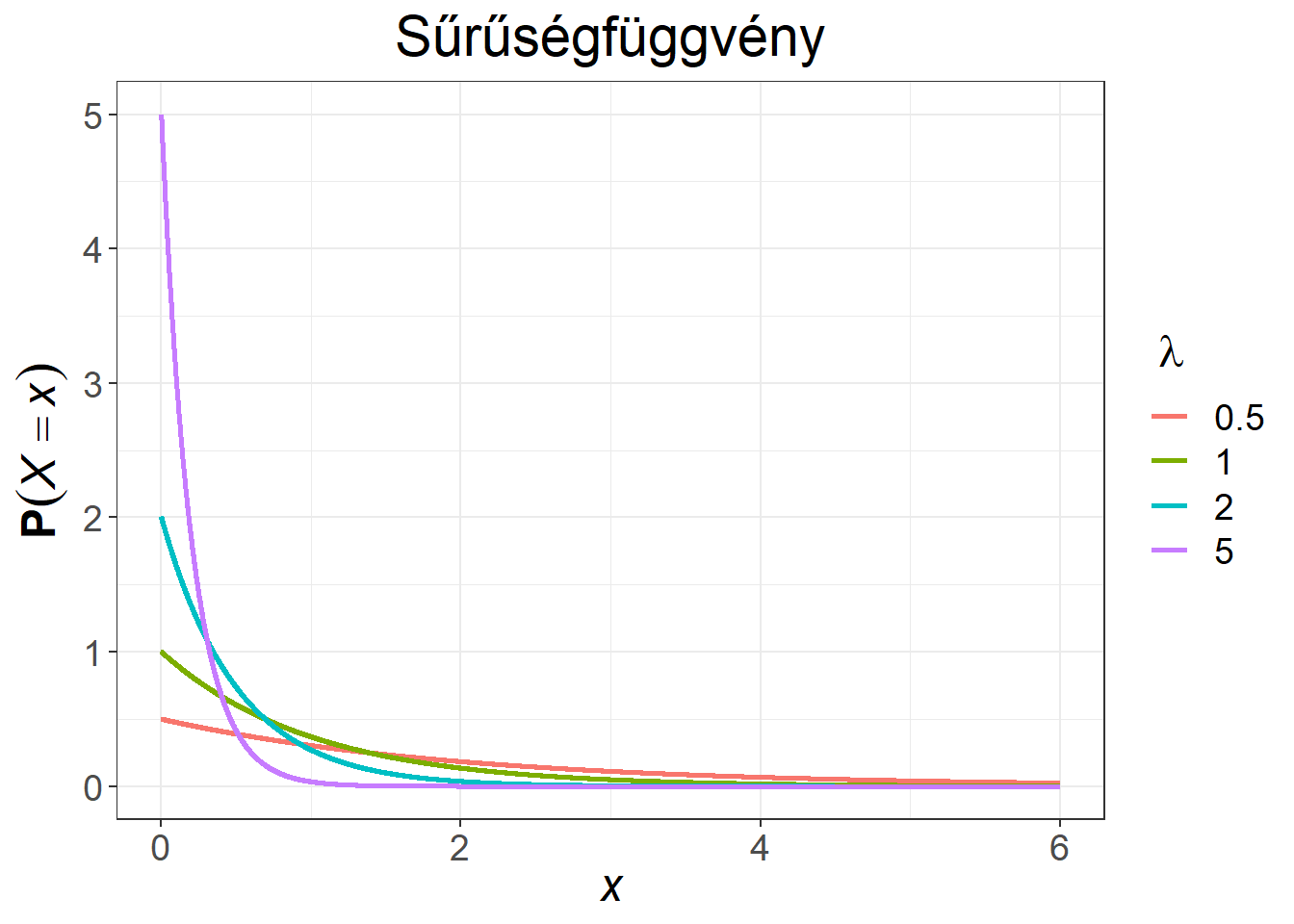
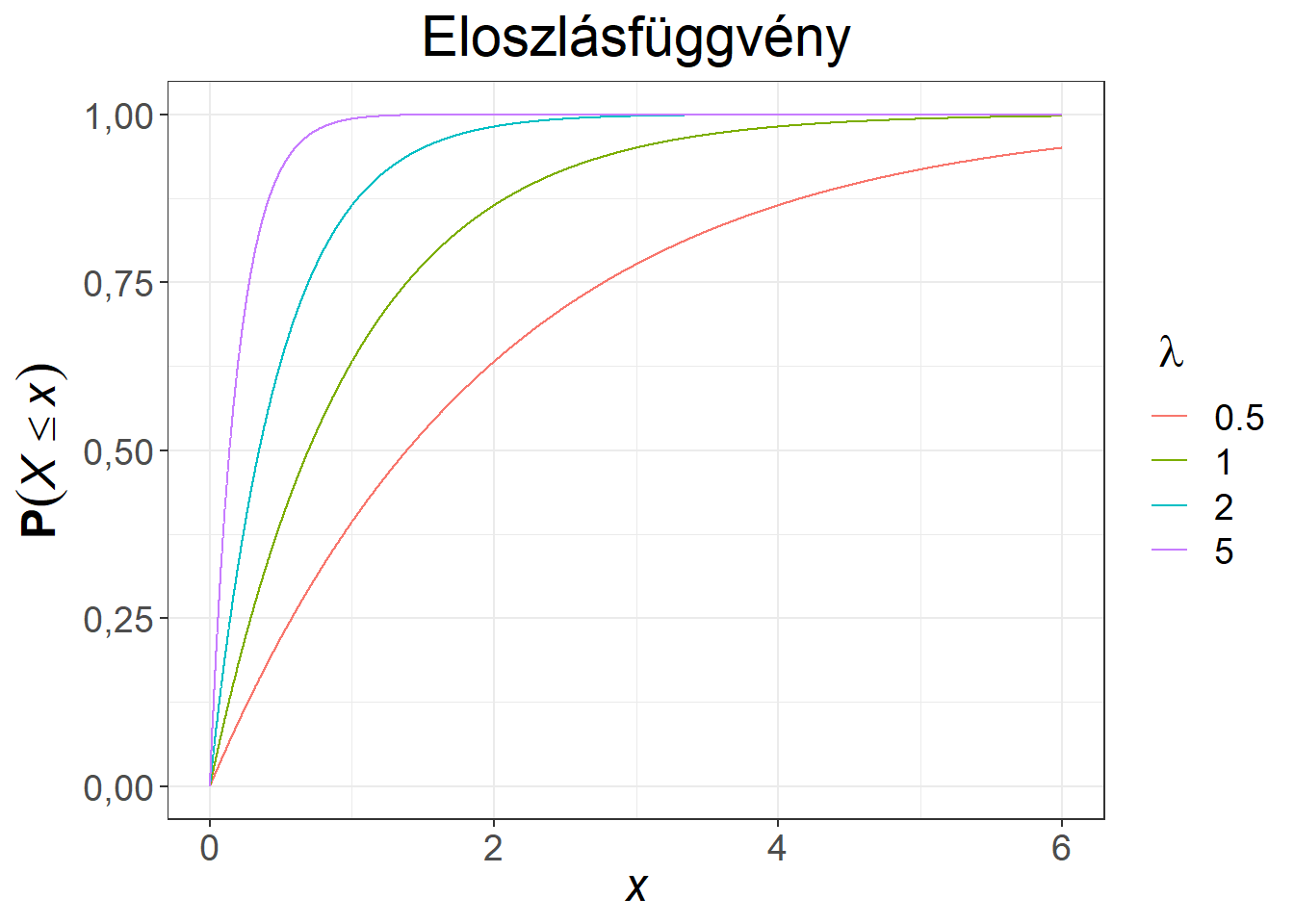
Ábra 6.4: Exponenciális eloszlású változó sűrűség- és eloszlásfüggvénye

6.3.3 Normális eloszlás

A normális eloszlás az egyik legfontosabb, leggyakrabban alkalmazott eloszlás. Ennek egyik oka, hogy a természetben is sok jelenség jó közelítéssel leírható ezzel az eloszlással, a másik ok, hogy a következtetéses statisztikában központi szerepet tölt be ez az eloszlás. A normális eloszlás két paraméterrel rendelkezik, melyeket \(\mu\) és \(\sigma\) jelöl (néhol \(\mu\) és \(\sigma^2\) paramétereket alkalmaznak), amely jelöléseket már alkalmaztunk a leíró statisztikával foglalkozó 2. fejezetben. A tananyag írásakor kínosan ügyelünk arra, hogy különböző fogalmakat ne jelöljünk ugyanazzal a betűvel, itt azonban mégis ezt tesszük, de a két paramétert klasszikusan ezekkel a betűkkel szokás jelölni, a későbbiekben kiderül, hogy miért. Legyen \(X\sim \mathcal{N}(\mu,\sigma)\), ekkor az eloszlás sűrűségfüggvénye:

\[\begin{equation} f(x)=\dfrac{1}{\sigma\sqrt{2\pi}}\mathrm{e}^{-\dfrac{1}{2}\left(\dfrac{x-\mu}{\sigma}\right)^2} \tag{6.11} \end{equation}\]

ahol \(x \in \mathbb{R}, \mu \in \mathbb{R}, \sigma>0\), \(\pi \approx 3{,}1416\) a Ludolph-féle szám, \(\mathrm{e} \approx 2{,}7182\) pedig az Euler-féle szám. A függvény a valós számok teljes körén értelmezett, így az \(X\) valószínűségi változó \(-\infty\) és \(\infty\) között elvileg bármilyen értéket felvehet. A \(\mu\) paraméter tetszőleges, a \(\sigma\) paraméter viszont nemnegatív. Az eddig megismert folytonos valószínűségi változókkal ellentétben az eloszlásfüggvény nem adható meg zárt alakban. A momentumok azonban a lehető legegyszerűbben számíthatóak, ugyanis

\[\begin{equation} \mathbf{E}(X)=\mu\qquad\mathbf{D}^2(X)=\sigma^2 \tag{6.12} \end{equation}\]

azaz azt tapasztaljuk, hogy a két paraméter értéke épp a várható értéket és a varianciát "állítja be", egymástól függetlenül. Éppen ez az a tulajdonság, ami miatt a jelölésük megegyezik a sokasági átlag és a sokasági variancia/szórás általunk is alkalmazott jelölésével.

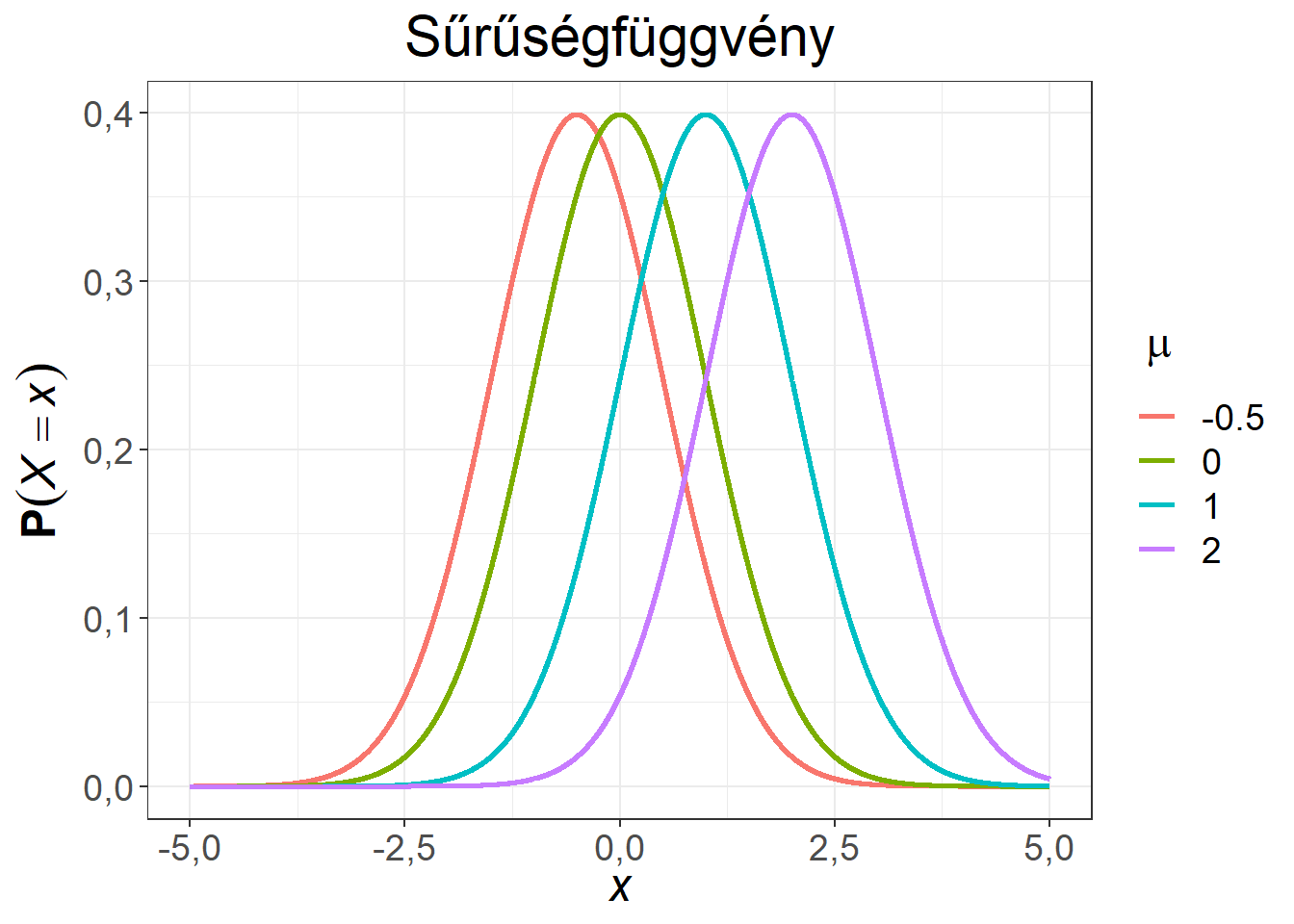
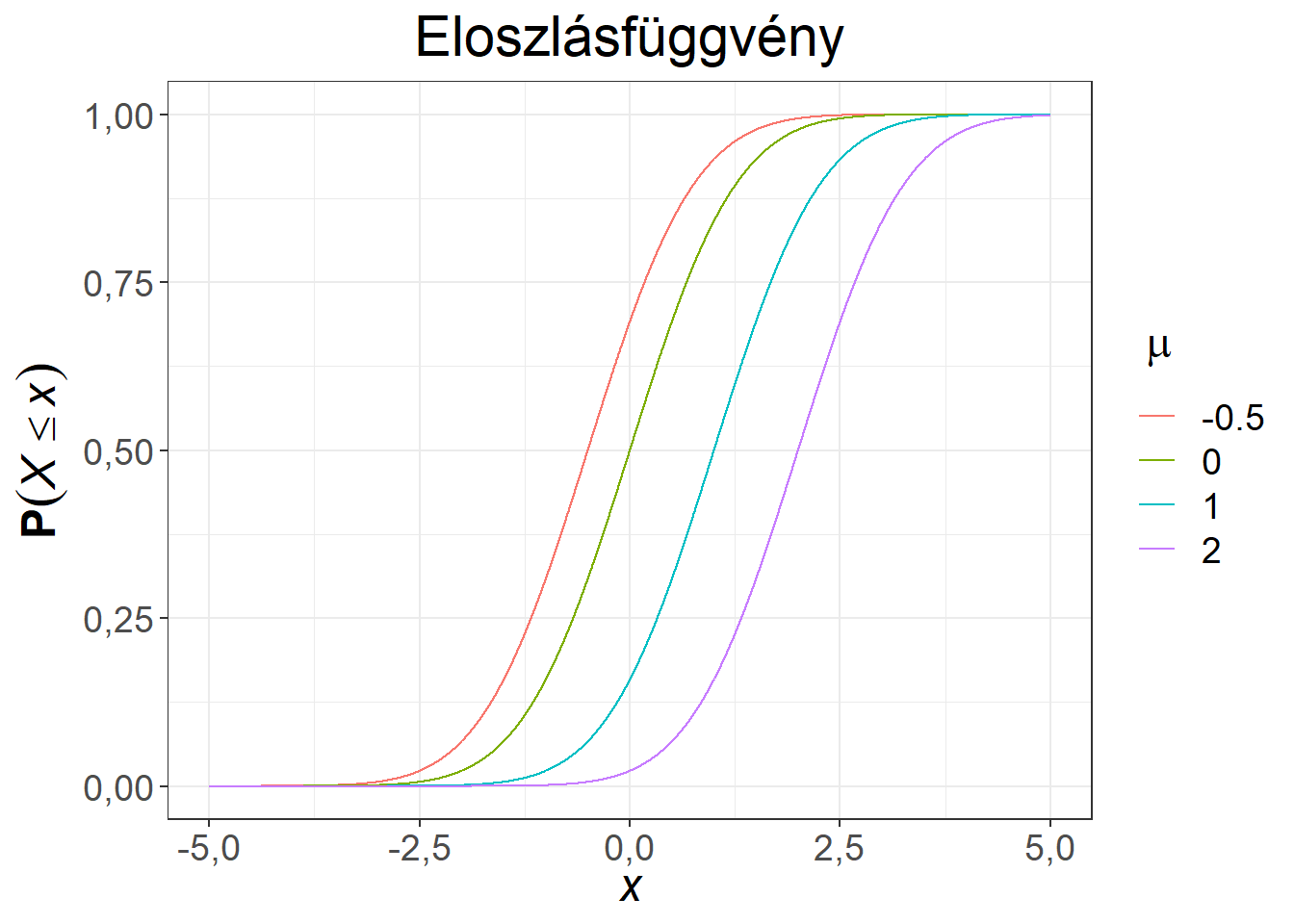
Ábra 6.5: Különböző várható értékű, 1 szórású normális eloszlások

Az ábrák alapján látható, hogy a normális eloszlás a \(\mu\) paraméterre szimmetrikus, illetve a módusza (a sűrűségfüggvény legmagasabb pontja) és a mediánja (a görbe alatti területet felező pont) is itt található. A függvények csupán eltolásban különböznek. Valamennyi esetben az értelmezési tartomány a teljes számegyenes, de a valószínűségek döntő része a \(-5, 5\) intervallumba esik ezekben a példákban.

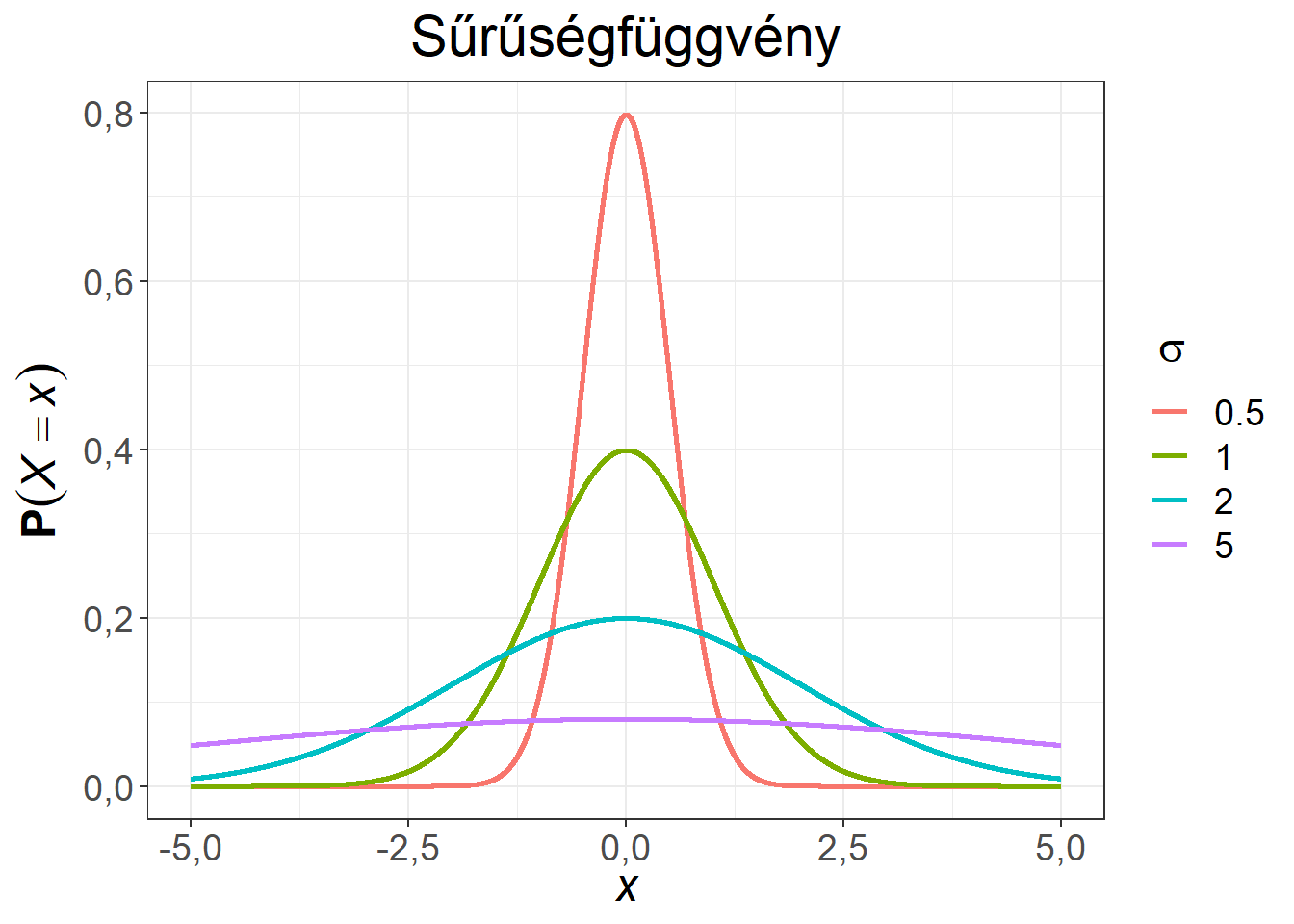
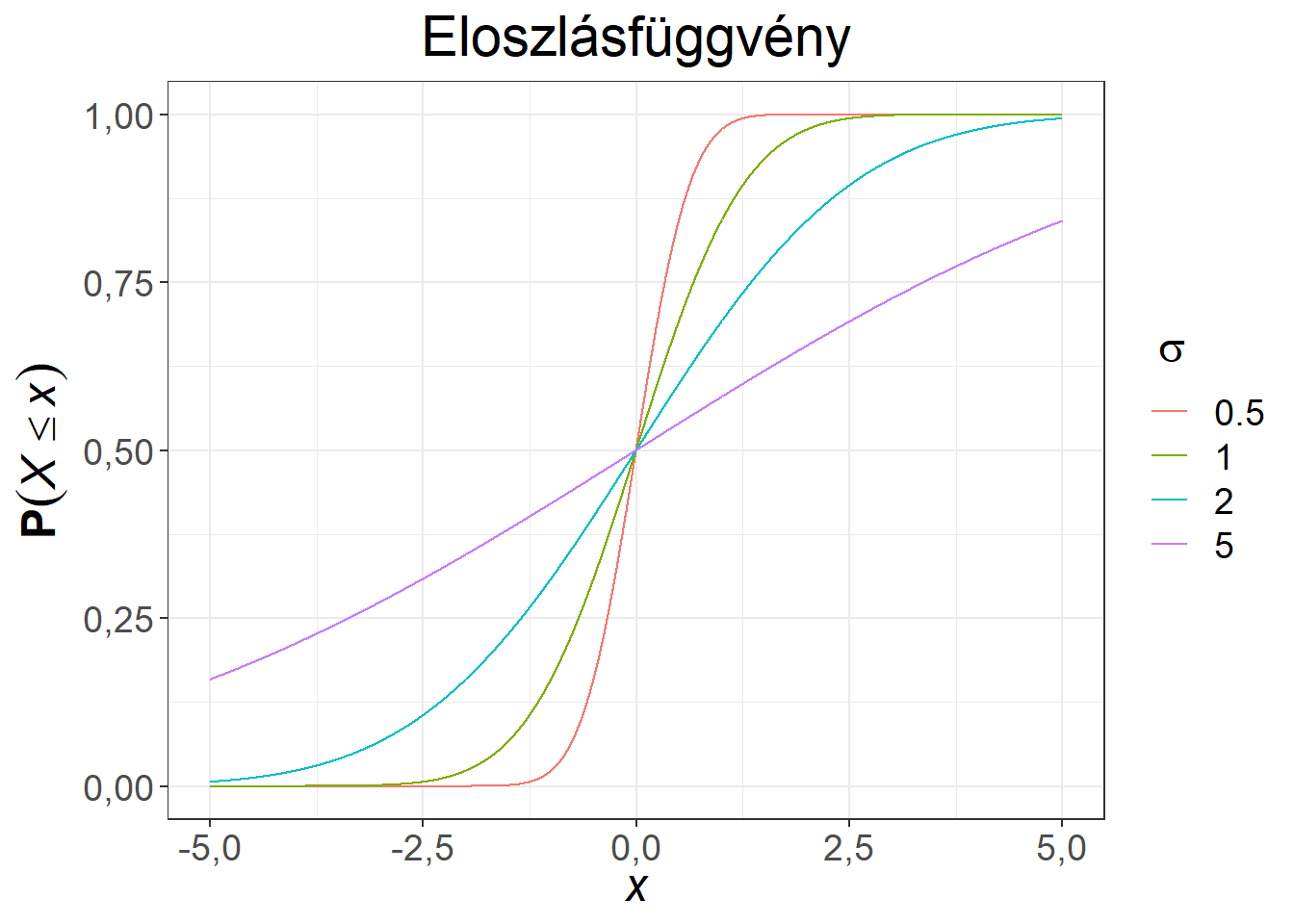
Ábra 6.6: Különböző szórású, 0 várható értékű normális eloszlások

Az azonos \(\mu\) paraméternek köszönhetően a sűrűségfüggvények azonos szimmetria tengellyel rendelkeznek, illetve valamennyi eloszlásfüggvény átmegy a (0; 0,5) ponton. Minél kisebb a \(\sigma\) paraméter értéke, jellemzően annál közelebb esnek az értékek a várható értékhez. A \(\sigma = 5\) paraméter mellett az eloszlás nagy része már nem fér rá a diagramra.

Legyen \(X \sim \mathcal{N}(100, 15)\), ami jó közelítéssel egy populáció IQ hányadosát leíró valószínűségi változó. Vegyük észre, hogy a feladat az IQ-t folytonos változóként kezeli, annak ellenére, hogy az IQ tesztek eredménye tipikusan egész szám. A modell feltételezése szerint az IQ nagyon sok lehetséges értéket vesz fel, az a mérőeszközünk jellemzője, hogy csak egész értékekre mér. Ebből azt tudjuk, hogy a legtöbb embernek 100 körül van az IQ-ja, illetve az emberek felének ennél alacsonyabb, a másik felének ennél az értéknél magasabb.

A normális eloszlás egyik fontos tulajdonsága, hogy a paraméterek értékétől függetlenül a várható érték adott szórásnyi környezetében minden esetben azonos terület található, ami a valószínűségek meghatározásában a későbbiekben segítségünkre lesz. Ahogy láttuk, az eloszlásfüggvénynek nincs zárt alakja, így ezeket a valószínűségeket numerikus úton lehetséges meghatározni (közelítés, szimuláció, stb.), ez azonban nem képezi tananyagunk részét. A valószínűségeket táblázat, vagy szoftver segítségével fogjuk meghatározni.

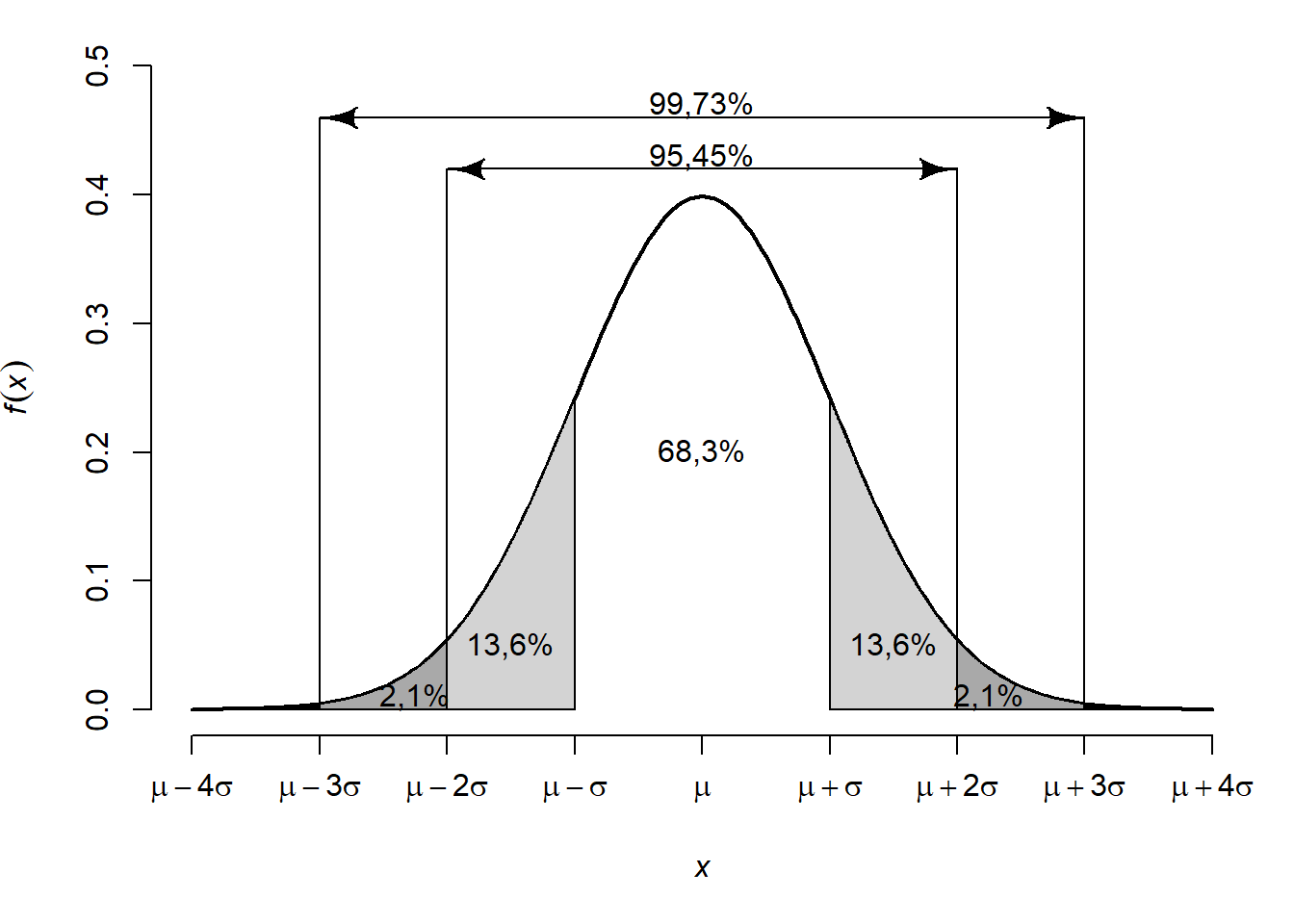
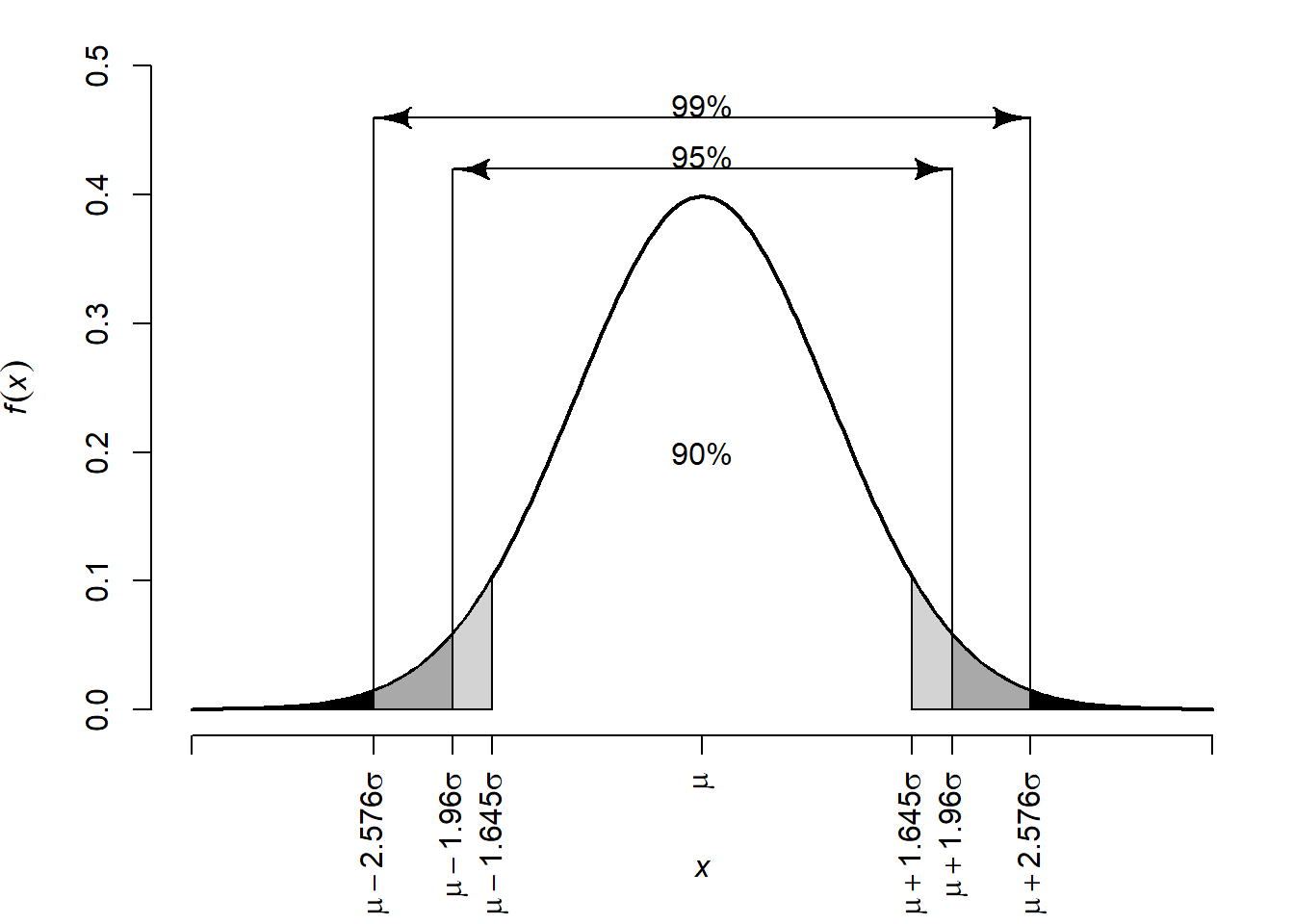
Ábra 6.7: Görbe alatti területek a várható érték körül

A 6.7. ábráról tehát azt olvashatjuk le, hogy -- függetlenül a paraméterek konkrét értékétől -- a várható érték egy szórásnyi környezetében a valószínűség mintegy 68,3%-a található, két \(\sigma\) esetén a valószínűség 95,45%, három \(\sigma\) esetén pedig már 99,73%. Gyakorlati szempontból nagyobb a jelentősége azoknak az eseteknek, ahol a valószínűség egy kerek, 1-hez közeli érték, a jobb oldali ábrán néhány ilyen eset látható. Ahhoz, hogy a terület 90%-át lefedjük a várható érték körül, 1,645 szórásnyit kell eltávolodnunk \(\mu\)-től mindkét irányban. 95%-os valószínűség eléréséhez 1,96, 99%-hoz pedig 2,576 szórásnyi távolság szükséges.

A normális eloszlás fenti jellemzői alapján tehát azt tudjuk, hogy a népesség mintegy 68,3%-ának 85 és 115 között van az IQ-ja, mintegy 95,5%-nak pedig 70 és 130 között. A szimmetria miatt az is meghatározható, hogy a fennmaradó 4,5% fele 70 alatti, fele pedig 130 feletti IQ-val rendelkezik. Amennyiben az emberek középső 90%-ának IQ-jára vagyunk kíváncsiak, úgy \(1{,}645 \cdot 15 = 24{,}675\) pontot kell a 100 várható értékből levonnunk, illetve hozzáadnunk.

A normális eloszlások közül kiemelt szerepe van a \(\mu = 0\) várható értékű, \(\sigma = 1\) szórású normális eloszlásnak, amit standard normális eloszlásnak nevezünk. Amint azt a normális eloszlás tulajdonságainál láttuk, a várható érték adott szórásnyi környezetében minden normális eloszlás esetén azonos valószínűség található. Ez lehetőséget ad arra, hogy egy kitüntetett normális eloszláson keresztül határozzuk meg a keresett valószínűségeket, méghozzá egy transzformáció -- a standardizálás -- segítségével. Mivel ezzel az eljárással minden normális eloszlás standard normálissá alakítható, ezért elegendő a standard normális eloszlás esetén egyszer meghatároznunk a különböző értékekhez tartozó valószínűségeket, majd ezeket egy táblázatba foglaljuk. Legyen tehát \(Z\sim \mathcal{N}(0,1)\), ekkor az eloszlás sűrűségfüggvénye:

\[\begin{equation} \phi(z)=\dfrac{1}{\sqrt{2\pi}}\mathrm{e}^{-\dfrac{1}{2}\left(z\right)^2} \tag{6.13} \end{equation}\]

ahol az általános (6.11) sűrűségfüggvénybe a \(\mu = 0\) és \(\sigma = 1\) helyettesítéseket végeztük el, illetve -- jelezve, hogy standardizált változóról van szó -- a változó elnevezésére \(X\) helyett \(Z\)-t használtunk. A sűrűségfüggvények általános \(f(x)\) jelölése helyett gyakran a \(\phi(z)\) jelölést alkalmazzuk, ami önmagában arra utal, hogy standard normális eloszlással van dolgunk. A standard normális eloszlás eloszlásfüggvényét ennek megfelelően a \(\Phi(z)\) módon jelöljük \(F(x)\) analógiájára. A \(\Phi(z)\) eloszlásfüggvénynek sincs ugyan zárt alakja, de léteznek táblázatok, melyek \(z\) bizonyos (pl. -3-tól 3-ig századonként) értékeire megadják az eloszlásfüggvény értékét, azaz a \(\mathbf{P}(Z \leq z)\) valószínűségeket. Néhány táblázat (például a tankönyvhöz tartozó képletgyűjteményben található) nem az eloszlásfüggvény értékét, hanem annak komplementerét tartalmazza, így feltétlenül szükséges a használt táblázat alapos ismerete. A táblázatok tipikusan a pozitív \(z\) értékeket tartalmazzák, az eloszlás szimmetriája miatt azonban a negatív \(z\) értékekre is alkalmazhatóak. Belátható, hogy minden \(z\)-re

\[\begin{equation} \Phi(z) = 1-\Phi(-z) \tag{6.14} \end{equation}\]

ami az eloszlás szimmetriája alapján grafikusan is könnyen ábrázolható.

Határozzuk meg annak a valószínűségét, hogy egy véletlenszerűen kiválasztott megfigyelés esetén az IQ 90-nél alacsonyabb! Tudjuk, hogy \(Z = \dfrac{X - \mu}{\sigma} \sim \mathcal{N}(0,1)\) és a normális eloszlás tulajdonságai alapján \[ \mathbf{P}(X < 90) = \mathbf{P}\left(Z < \dfrac{90-100}{15}\right) = \mathbf{P}\left(Z < -\dfrac{2}{3}\right) = \Phi\left(-\dfrac{2}{3}\right) \]

A (6.14) alapján tehát \[ \mathbf{P}(X < 90) = 1 - \Phi\left(\dfrac{2}{3}\right) \] azaz az eloszlásfüggvény értékeit tartalmazó táblázatból a 0,67 helyen található valószínűség komplementerét keressük. Az eloszlásfüggvény komplementerét tartalmazó táblázatból azonban közvetlenül kiolvasható a keresett valószínűség, ami 0,2514. Az Excel, illetve a statisztikai programok a keresett valószínűséget közvetlenül (az eredeti eloszlásból) is képesek szolgáltatni, nem csupán két tizedes figyelembevételével, de fontosnak tartjuk a táblázat ismeretét is.

Sok esetben nem egy \(x\) érték alapján keresünk valószínűséget, hanem fordítva, azt az \(x\) értéket keressük, amelyhez adott valószínűség tartozik. Ezt az eloszlásfüggvény inverzének nevezzük. Az eloszlásfüggvény zárt alakjának hiánya miatt alapvetően itt is a standard normális eloszláshoz tartozó táblázatra támaszkodhatunk, épp fordítva gondolkodva. A táblázat belsejében keressük meg a leginkább megfelelő valószínűséget (nem feltétlenül találjuk meg egészen pontosan a keresett értéket), majd ehhez keressük meg \(z\)-t. A standardizálás műveletét is épp fordítva végezzük el, amennyiben \(Z\sim \mathcal{N}(0,1)\), úgy \(\mu + Z \sigma = X \sim \mathcal{N}(\mu, \sigma)\).

Határozzuk meg azt az \(x\) értéket, melynél az emberiség csupán 1%-ának magasabb az IQ-ja! Ehhez elsőként azt a \(z\) értéket keressük, melyre igaz az ekvivalens állítás, miszerint az értékek 99%-a alacsonyabb nála. \[ \Phi(z) = \mathbf{P}(Z \leq z) = 0{,}99 \] ekkor a \[ z = \Phi^{-1}(0{,}99) \] megoldást (az eloszlásfüggvény inverzét) keressük. A táblázat alapján a keresett \(z\) érték 2,32 és 2,33 között található (0,0102 és 0,0099 valószínűség tartozik a két \(z\) értékhez). A 2,33 értékkel számolva a keresett IQ \[ x = \mu + \sigma z = 100 + 15 \cdot 2{,}33 = 134{,}95 \] Ez az az IQ érték tehát, aminél az emberiség csupán 1%-ának magasabb az intelligenciahányadosa.