3.1 Kvantilisek

A kvantilisek egyik tagjával, a mediánnal már találkoztunk a 2.2.5. fejezetben, amit sokasági felezőpontként definiáltunk. A sokaságot azonban nem csak két, hanem akár több egyenlő részre tudjuk bontani, ezeket az általános osztópontokat hívjuk kvantiliseknek. Attól függően, hogy hány részre osztják a sokaságot

• tercilis (harmadoló - jele \(T_t \quad t=1,2\)),
• kvartilis (negyedelő - jele \(Q_q \quad q=1,2,3\)),
• kvintilis (ötödölő - jele \(K_k \quad k=1,2,3,4\)),
• decilis (tizedelő - jele \(D_d \quad d=1,2,\dots,9\)),
• percentilis (századoló - jele \(P_p \quad p=1,2,\dots,99\))

névvel illetjük a kvantiliseket. A tercilis tehát például három egyenlő részre bontja a sokaságot, abban az értelemben, hogy mind a három harmadban a sokaság (közel) azonos számú eleme található. A sorba rendezett értékek közül tehát egy adott algoritmus alapján azokat az értékeket határozzuk meg, melyeknél a sokasági egyedek harmada kisebb, illetve nagyobb. Tercilisből tehát kettő van, a \(T_1\) és \(T_2\) jelöléseket használhatjuk. A leggyakrabban alkalmazott kvantilisek talán a kvartilisek, azaz a negyedelőpontok. Definíció szerint \(Q_1\) azt az értéket jelöli, amelynél a megfigyelések negyede kisebb, háromnegyede pedig nagyobb, elnevezése első, vagy alsó kvartilis. A második kvartilis egyben a medián, a felső, vagy harmadik kvartilis jele \(Q_3\). Hasonlóan definiálhatunk ötödölő és tizedelő osztópontokat, amiből rendre 4, illetve 9 értelmezhető. A legáltalánosabb (hiszen valamennyi fent említett kvantilis előállítható speciális eseteként) nevesített kvantilis a percentilis, azaz századoló pont, ennek segítségével tetszőleges százalékos felosztás készíthető a sokaságról.

Fontos tehát, hogy két szomszédos kvantilis között mindig a sokaság adott hányada (harmada, negyede, ötöde, stb. található), az azonban nem feltétlenül igaz (sőt, szinte soha nem igaz!), hogy a szomszédos kvantilisek közötti távolság azonos. Ne felejtsük el, a fejezetben a cél a sokasági értékek elhelyezkedésének vizsgálata, az osztópontok elhelyezkedése, távolsága pontosan az az információ, ami segít ezt megérteni.

Amennyiben "kézzel" szeretnénk például kvartiliseket meghatározni, úgy nagyon hasonlóan járunk el, mint a medián (lásd 2.2.5. fejezet) esetén, az alsó kvartilis esetén a sorba rendezett sokaság \(\dfrac{N+1}{4}\)-edik, míg a felső kvartilis esetén a \(\dfrac{3\left(N+1\right)}{4}\). értéket keressük meg. Amennyiben a képletek egész sorszámot adnak meg, úgy meg is találtuk a keresett értékeket. Ahogy már a medián esetén is megkülönböztettük a páros és páratlan elemszámú sokaságokat, úgy ebben az esetben a néggyel való osztási maradék alapján négy esetet is megkülönböztethetnénk. A helyzet tovább bonyolódik, ha például percentilist szeretnénk meghatározni.

A legegyszerűbb, ha az alábbi (némileg önkényes) elvet követjük tetszőleges kvantilis közelítő kiszámítása esetén:

• amennyiben a keresett érték sorszáma egész, úgy egyszerűen válasszuk ki az adott értéket a sorba rendezett sokaságban,
• amennyiben a keresett sorszám ,5-re végződik, vegyük a két szomszédos megfigyelés átlagát (ahogy a mediánnál is tettük),
• minden más esetben kerekítsük a sorszámot a legközelebbi egészre és az annak megfelelő elemet válasszuk a sokaságból.

Egy másik lehetőség az lenne, ha arányosítanánk a két szóban forgó megfigyelés közötti távolságot. Látható, hogy több különböző elv, algoritmus van a kvantilisek kiszámítására, ennek megfelelően Excelben két, míg az R-ben 9, némileg eltérő eredményt adó függvény került implementálásra, a köztük lévő különbség taglalása meghaladja tananyagunk kereteit.

Tegyük fel, hogy a kvartiliseket keressük egy \(N = 11\) elemű sokaságban. Ekkor az alsó kvartilis sorszáma \(\dfrac{N+1}{4} = 3\), azaz a sorba rendezett sokaság 3. eleme, a 6. eleme a medián, és minthogy \(\dfrac{3\left(N+1\right)}{4} = 9\), a 9. elem a felső kvartilis. Újra nyomatékosítani szeretnénk, hogy nem a kvartiliseket és a mediánt számoltuk ki, csupán a keresett sokasági elemek sorszámát!

Legyen most a sokaság \(N = 20\) elemű. Ekkor a fenti szabályok szerint \(\dfrac{N+1}{4} = 5{,}25\), ami kerekítve 5, azaz az ötödik elemet keressük, míg \(\dfrac{3\left(N+1\right)}{4} = 15{,}75\), azaz a 16. elemet keressük és azonosítjuk őket kvartilisként.

Ne felejtsük el, hogy az egyszerű kerekítés helyett más szabályok is vannak, azaz ha szoftverrel számítjuk a kvantiliseket, némileg eltérő eredményeket kaphatunk!

Amint azt már említettük, gyakran alkalmazzuk a kvartiliseket, egyrészt azért mert a kvartilisek távolságára épül egy szóródási mérőszám, az interkvartilis terjedelem, másrészt egy gyakran használt statisztikai ábra, a boxplot is felhasználja az értékeket.

Az interkvartilis terjedelem kiküszöböli a terjedelem mutató azon hibáját, hogy túl érzékeny a kiugró adatokra, az interkvartilis terjedelem ugyanis csak a sokaság középső 50%-ának terjedelmét vizsgálja:

\[\begin{equation} \text{IQR}=Q_3-Q_1 \tag{3.1} \end{equation}\]

Az interkvartilis terjedelem mutatójának mértékegysége megegyezik az eredeti adatok mértékegységével. Amennyiben a sokaság nem szóródik, azaz minden eleme megegyezik, az IQR mutató értéke 0 (az állítás fordítva nem feltétlenül igaz).

A boxplot (a magyar doboz diagram kifejezés nem igazán terjedt el) a sokaság öt jellemző értékének (five number summary) grafikus megjelenítése, amely alkalmas különböző sokaságok, vagy csoportok eloszlásának összehasonlítására. Az ábrának több, kissé eltérő változata is létezik, de az valamennyi esetben közös, hogy az alábbi öt érték feltüntetésre kerül:

• \(X_{(1)}\)
• \(Q_1\)
• \(\text{Me}\)
• \(Q_3\)
• \(X_{(N)}\)

Az ábra felépítése egy \(Q_1\) és \(Q_3\) közötti dobozból (innen az elnevezés), a mediánnál egy ezen áthaladó vonalból, valamint a dobozból kinyúló "bajszokból" (angolul box-and-whisker plot néven is ismert) áll a minimum és a maximum irányában. Néhány szoftver a medián mellett az átlagot is jelöli egy ponttal, vagy kereszttel, illetve sok esetben a kiugró értékekként érzékelt megfigyelések (lásd 2.4. fejezet, bár az outliereket általában nem a z-score, hanem az \(\text{IQR}\) segítségével azonosítják) is különálló pontokként szerepelnek, ami miatt a bajusz rövidebb lesz. A boxplotokat vízszintesen és függőlegesen is rajzolhatjuk. A 3.1. ábrán a fejezet elején definiált öt sokaság boxplot ábráját tüntettük fel, ezek emlékeztetőül:

1. szimmetrikus, nem túl lapos, nem túl csúcsos
2. szimmetrikus, lapult eloszlás
3. szimmetrikus, csúcsos eloszlás
4. jobboldali aszimmetria, csúcsos eloszlás
5. baloldali aszimmetria, csúcsos eloszlás

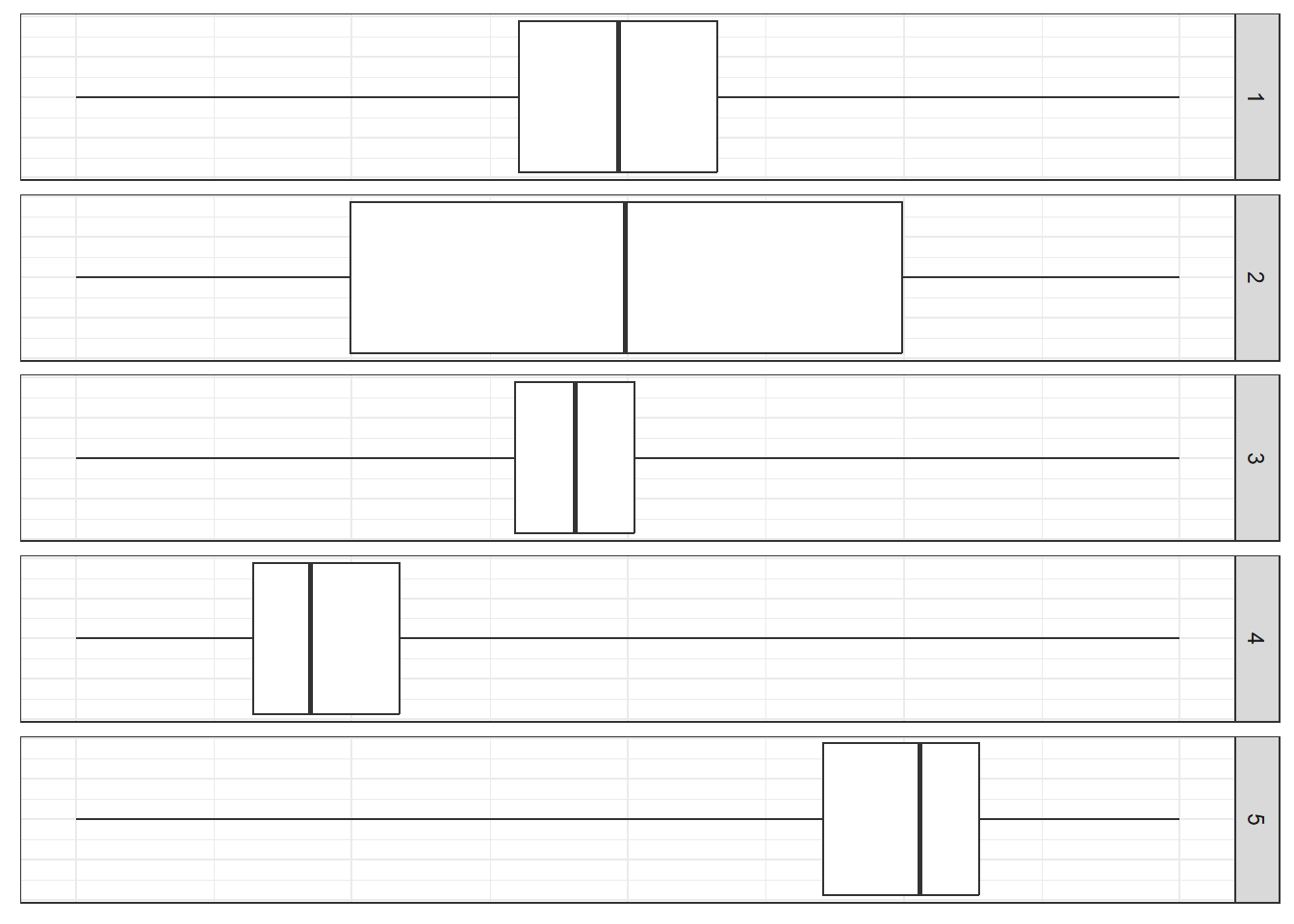
Ábra 3.1: Különböző eloszlással rendelkező sokaságok alapján készített boxplotok

A TOP100 brandérték példánkra visszatérve: azt már korábban láttuk, hogy az átlag (43,835) jelentősen meghaladja a mediánt (23,2955), tehát várhatóan jobboldali aszimmetriáról fog tanúskodni a boxplot. A terjedelem kiszámításánál (2.3.1. fejezet) láttuk, hogy a minimum 12,456, a maximum pedig 302,063, azaz a medián jóval közelebb helyezkedik el a minimumhoz, mint a maximumhoz. Az alsó kvartilis értéke mintegy 17,6 (a pontos érték az alkalmazott képlettől függ), míg a felső kvartilis mintegy 41,4 milliárd dollár. Azaz a TOP100 márkaértékkel rendelkező vállalatok negyedének értéke 17,6 milliárd dollár alatti, háromnegyedüknek ezt az értéket meghaladja, illetve a vállalatok negyedének haladja meg az értéke a 41,4 milliárd dollárt. A TOP100 brandérték alapján készült boxplotot mutatja be a 3.2. ábra. Míg bal oldali ábra egy kiugró értékeket külön nem jelölő, függőlegesen elhelyezkedő boxplot, addig a jobb oldalon a kiugrónak ítélt megfigyeléseket pontokkal jelöltük a vízszintes tengelyen helyeztük el az ábrázolandó értékeket.

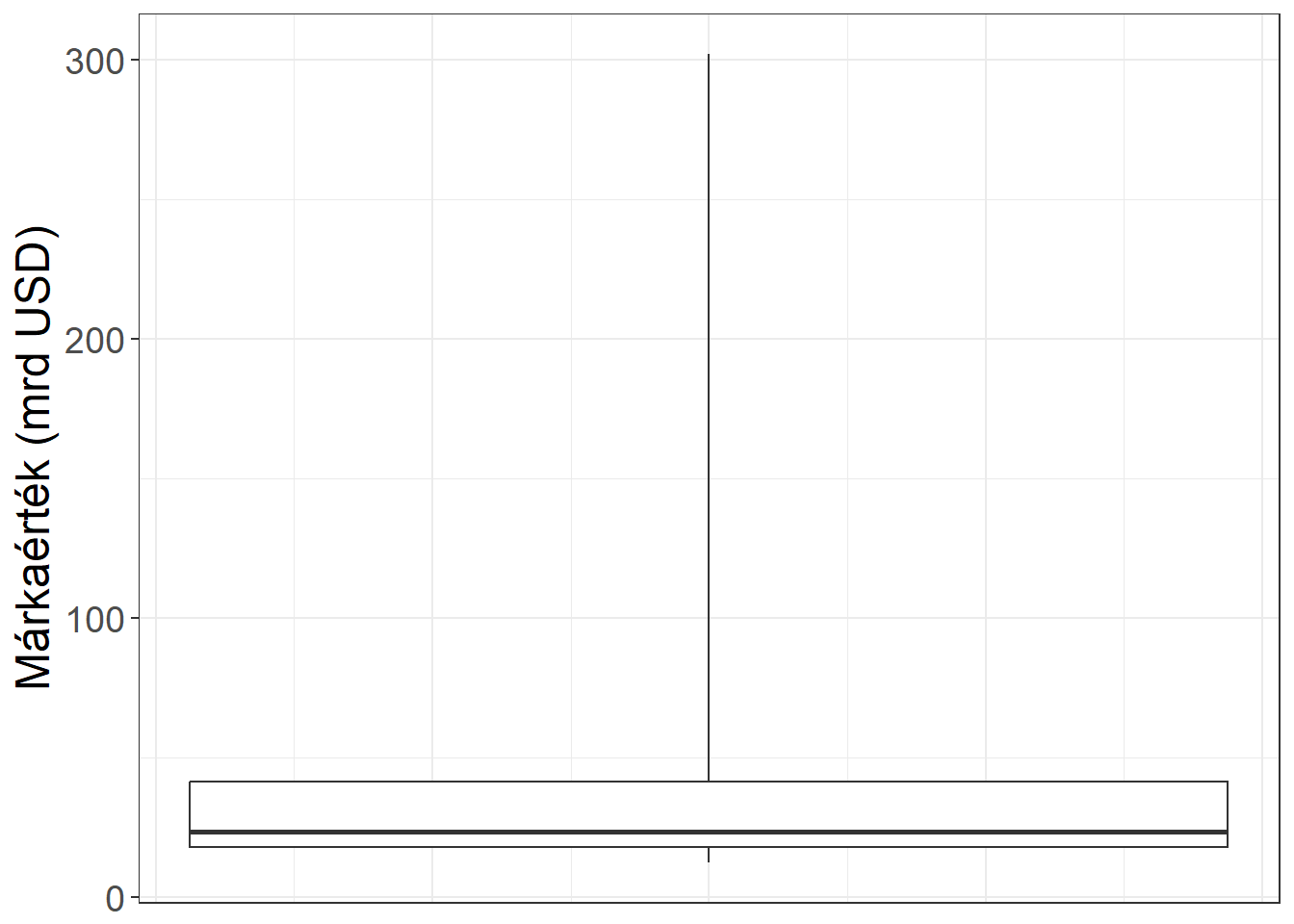
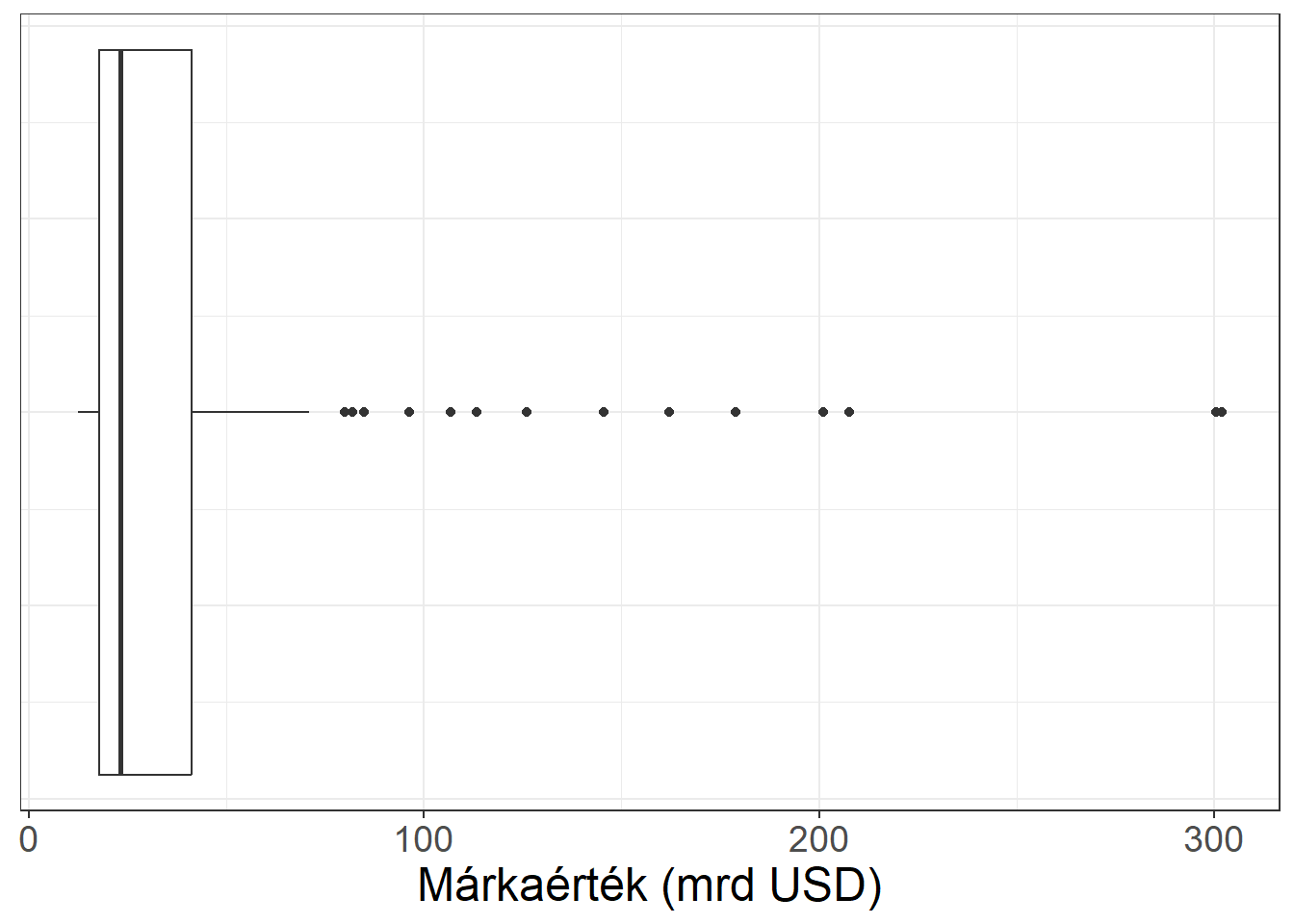
Ábra 3.2: A márkaértékek boxplotja

Összefoglalóan tehát a kvantilisek tetszőleges osztópontokat jelölnek, melyek önmagukban is alkalmasak elemzésre, a leggyakrabban a kvartiliseket használja a statisztika, elsősorban a boxplot megalkotására. A boxplot alakjából következtetünk a sokasági megfigyelések elhelyezkedésére, a jobboldali aszimmetria esetén hosszú jobb oldali (vagy fenti) bajuszt és akár sok kiugró értéket látunk. A sokaság lapult, ha mind a doboz, mind pedig a bajszok viszonylag nagyok, illetve csúcsos, ha a box (vagyis az interkvartilis terjedelem), vagy valamelyik bajusz nagyon rövid. Ne feledjük, bármely két szomszédos kvartilis között a sokaság elemeinek negyede található meg!