5.1 Súly- és eloszlásfüggvény
A fejezetben a diszkrét valószínűségi változók jellemzésére szolgáló két eszközt, a súlyfüggvényt és az eloszlásfüggvényt mutatjuk be.
Egy \(X\) diszkrét valószínűségi változó súlyfüggvénye alatt a
\[\begin{equation} \mathbf{P} \left( X = x_k\right) = p_k \tag{5.1} \end{equation}\]
függvényt értjük, ami egy tetszőleges valós számhoz az érték bekövetkezési valószínűségét rendeli. A hozzárendelést megadhatjuk az összes lehetséges érték, és a valószínűségek felsorolásával, vagy akár képletek segítségével is, ahogy azt a 5.3. pontban látni fogjuk.
Diszkrét valószínűségi változók esetén az \(x_k\) lehetséges értékeket gyakran \(k\)-val jelöljük, jelezve, hogy csak természetes számok esetén vesz fel a függvény 0-tól különböző értéket. Emiatt a fejezetben gyakran fogunk élni a \(\mathbf{P} \left( X = k\right) = p_k\) egyszerűsített jelöléssel.
A \(p_k\) valószínűségeknek két feltételt kell teljesíteniük ahhoz, hogy egy diszkrét eloszlást írjanak le:
- \(p_k \geq 0\), azaz a valószínűségek nemnegatívak,
- \(\sum_k p_k = 1\), mivel a lehetséges értékek teljes eseményrendszert alkotnak.
Ha a szóban forgó kísérletet nagyon sokszor elvégezzük, akkor a megfigyelt relatív gyakoriságok a valószínűségekhez fognak tartani. A súlyfüggvény ábrázolására jellemzően oszlop-, vagy pálcikadiagramot használhatunk.
Az egyik legegyszerűbb diszkrét valószínűségi változó a kockadobás példájához tartozik, ebben az esetben a súlyfüggvény \[ p_1 = p_2 = \dots = p_6 = \dfrac{1}{6} \] ami azt jelenti, hogy ha nagyon sok kockadobást végeznénk el, akkor azt várjuk, hogy minden dobott szám megközelítőleg \(\dfrac{1}{6}\) relatív gyakorisággal fog előfordulni.
Egy \(X\) diszkrét valószínűségi változó eloszlásfüggvénye alatt a
\[\begin{equation} F(x) = \mathbf{P} \left( X \leq x\right) \tag{5.2} \end{equation}\]
függvényt értjük, ami egy tetszőleges valós számhoz az \(X \leq x\) esemény bekövetkezési valószínűségét rendeli. Az eloszlásfüggvény a diszkrét esetben nem annyira fontos, hiszen a súlyfüggvény segítségével könnyedén meghatározhatók a szükséges valószínűségek, de a folytonos eloszlásoknál definiált eloszlásfüggvény kiemelten fontos lesz a következő fejezetben, ezért már itt is megemlítjük. Diszkrét esetben az eloszlásfüggvény értéke az \(a\) helyen (\(F\left(a\right)\)) egyszerűen azon súlyfüggvény-értékek összege, melyekre az \(x_k \leq a\) feltétel teljesül.
Az egyik legegyszerűbb diszkrét valószínűségi változó a kockadobás példájához tartozik, ebben az esetben az eloszlásfüggvény néhány pontja például:
\(F(2) = \mathbf{P} \left( X \leq 2\right) = \mathbf{P} \left( X = 1\right) + \mathbf{P} \left( X = 2\right) = p_1 + p_2 = \dfrac{1}{3}\)
\(F(4{,}5) = \mathbf{P} \left( X \leq 4{,}5\right) = p_1 + p_2 + p_3 + p_4 = \dfrac{2}{3}\)
Az eloszlásfüggvény monoton növekvő, hiszen \(x\) növelésével a \(\mathbf{P} \left( X \leq x\right)\) valószínűség nem csökkenhet. A diszkrét értékek között a függvény szakaszonként konstans, hiszen például az \(F(4{,}5)\) és az \(F(4{,}8)\) valószínűségek megegyeznek. A függvény határértéke \(-\infty\)-ben 0, \(\infty\)-ben pedig egy, azaz minél nagyobb \(x\)-re a valószínűség minden határon túl megközelíti (vagy eléri) az egyet. Ahogy a súlyfüggvény statisztikai megfelelője a relatív gyakoriság, úgy az eloszlásfüggvény esetében ezt a szerepet a kumulált relatív gyakoriság tölti be.
Könnyen belátható, hogy az eloszlásfüggvény akkor igazán hasznos, ha a kiszámítandó valószínűség nem \(\mathbf{P} \left( X = x\right)\) típusú, hanem egy nyílt, vagy zárt intervallumba esés valószínűségét szeretnénk kiszámítani. Az alábbiakban bizonyítás nélkül mutatjuk be azokat az eseteket egy táblázatban, melyek esetén az eloszlásfüggvény is alkalmazható. Természetesen minden valószínűség megadható a megfelelő súlyfüggvényértékek összeadásával is.
| keresett valószínűség | alkalmazható formula |
|---|---|
| \(\mathbf{P} \left( X \leq a\right)\) | \(F(a)\) |
| \(\mathbf{P} \left( X < a\right)\) | \(F(a-1)\) |
| \(\mathbf{P} \left( X \geq a\right)\) | \(1 - F(a-1)\) |
| \(\mathbf{P} \left( X > a\right)\) | \(1 - F(a)\) |
| \(\mathbf{P} \left(a < X \leq b\right)\) | \(F(b) - F(a)\) |
| \(\mathbf{P} \left(a \leq X \leq b\right)\) | \(F(b) - F(a-1)\) |
| \(\mathbf{P} \left(a < X < b\right)\) | \(F(b-1) - F(a)\) |
| \(\mathbf{P} \left(a \leq X < b\right)\) | \(F(b-1) - F(a-1)\) |
A súlyfüggvény és az eloszlásfüggvény szoros kapcsolatban állnak egymással, ahogy láttuk, az eloszlásfüggvény előállítható a súlyfüggvény megfelelő értékeinek összeadásával.
A kockadobás példájához tartozó súlyfüggvény és az eloszlásfüggvény az 5.1. ábrán látható. A súlyfüggvény azt mutatja meg, hogy a valószínűségek hol helyezkednek el, míg az eloszlásfüggvény egy lépcsős, szakaszonként konstans függvény képét mutatja. A két függvény egymással szorosan összefügg, az egyikből kiszámítható a másik, összeadás, illetve ennek inverz művelete, kivonás segítségével: az eloszlásfüggvényben ott van ugrás, ahol lehetséges érték van, ennek a lehetséges értéknek a valószínűsége pedig az ugrás nagyságával azonos.
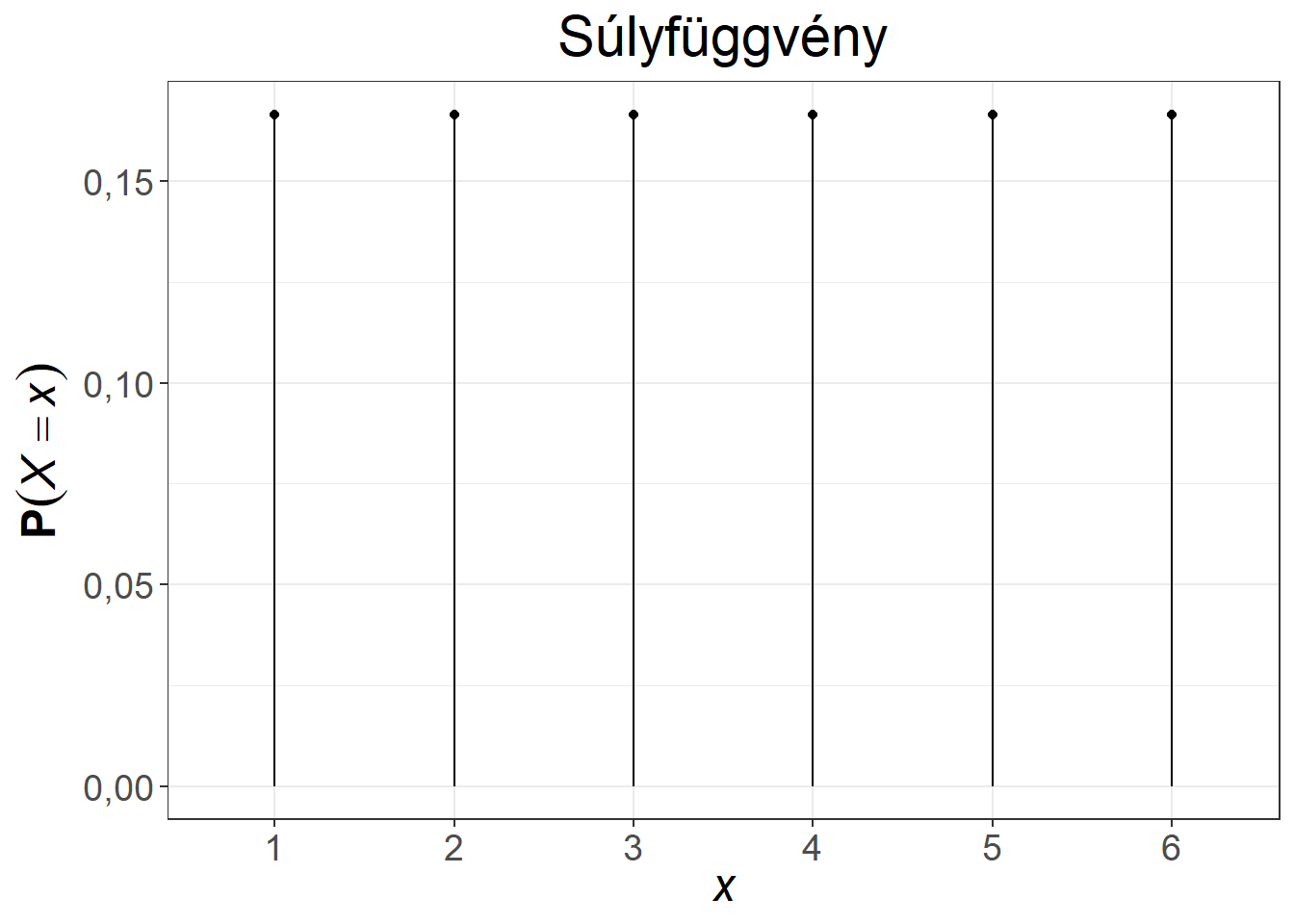
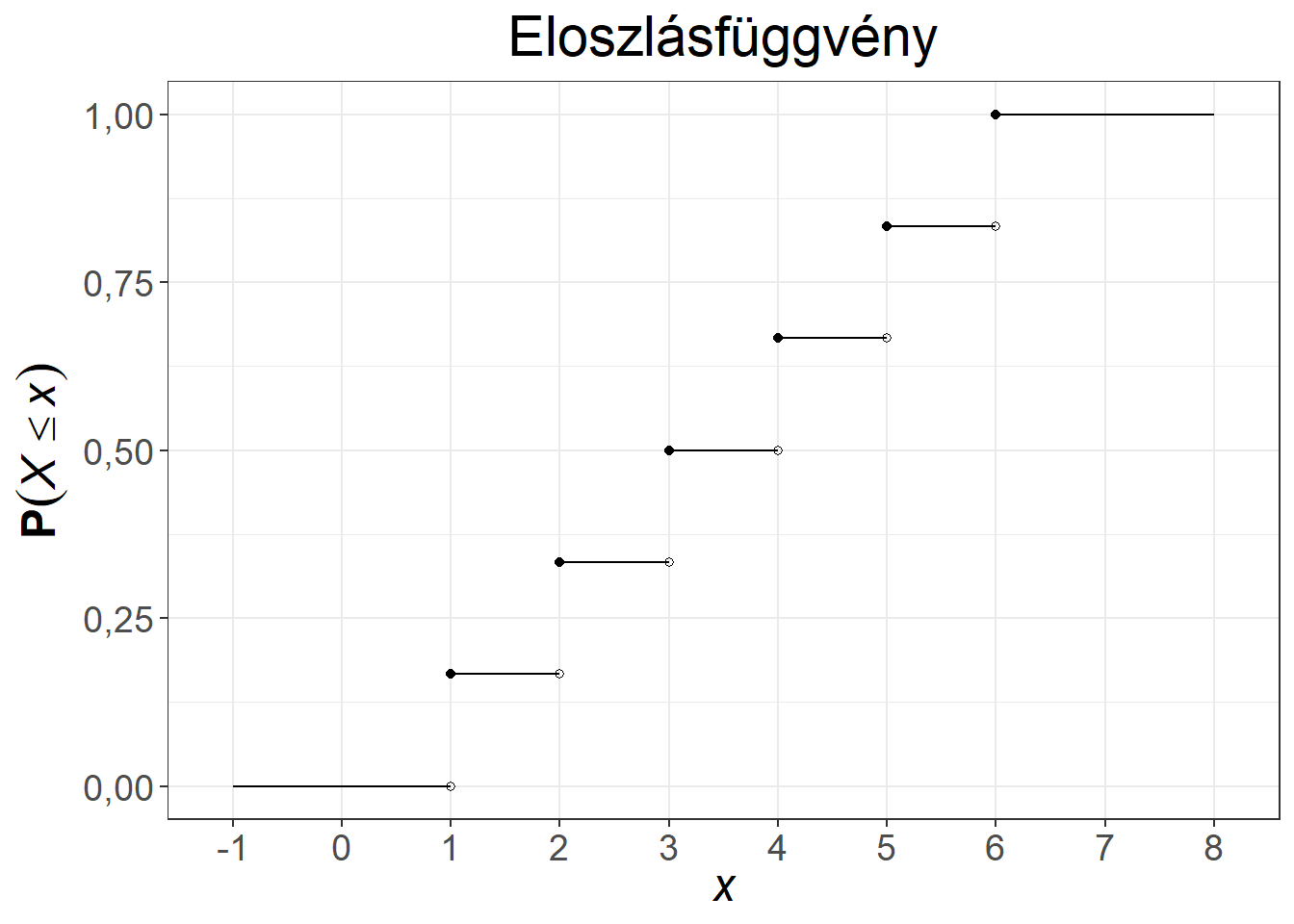
Ábra 5.1: A kockadobás valószínűségi változójának súly- és eloszlásfüggvénye