7.1 Kétváltozós diszkrét eloszlások
A fejezetben a kétváltozós diszkrét eloszlásokhoz kapcsolódó fogalmakat és elemzési eszközöket mutatunk be. A fogalmak egy része az 5. fejezetben megismertek általánosítása, a több valószínűségi változó együttes vizsgálata azonban lehetőséget ad azok kapcsolatának vizsgálatára is, amire a statisztika is nagy mértékben támaszkodik.
Jelölje \((X, Y)\) a kétváltozós, mindkét változójában diszkrét vektorváltozót (többváltozós esetben célszerűbb indexeket alkalmazni a változók jelölésére \((X_1, X_2, \dots, X_k)\)). Jelölje továbbá rendre \(x_i\) és \(y_j\) a lehetséges értékeket.
7.1.1 Súly- és eloszlásfüggvény
A valószínűségi vektorváltozókat az egyváltozós esethez hasonlóan jellemezhetjük a lehetséges értékek, valamint azok valószínűségének felsorolásával. Jelölje az együttes bekövetkezési valószínűségeket
\[\begin{equation} \mathbf{P} \left( X = x_i, Y = y_j\right) = p_{ij} \tag{7.1} \end{equation}\]
amivel tulajdonképp a kétváltozós diszkrét eloszlás súlyfüggvényét definiáltuk. A két változó együttes eloszlását (azaz a lehetséges értékeket és valószínűségeiket) érdemes egy táblázat segítségével összefoglalni:
| \(X, Y\) | \(y_1\) | \(y_2\) | \(\dots\) | \(y_m\) | \(\mathbf{P}(X=x_i)\) |
|---|---|---|---|---|---|
| \(x_1\) | \(p_{11}\) | \(p_{12}\) | \(\dots\) | \(p_{1m}\) | \(p_{1.}\) |
| \(x_2\) | \(p_{21}\) | \(p_{22}\) | \(\dots\) | \(p_{2m}\) | \(p_{2.}\) |
| \(\dots\) | \(\dots\) | \(\dots\) | \(\dots\) | \(\dots\) | \(\dots\) |
| \(x_n\) | \(p_{n1}\) | \(p_{n2}\) | \(\dots\) | \(p_{nm}\) | \(p_{n.}\) |
| \(\mathbf{P}(Y=y_j)\) | \(p_{.1}\) | \(p_{.2}\) | \(\dots\) | \(p_{.m}\) | 1 |
Természetesen a fenti valószínűségekre minden \(i\) és \(j\) esetén \(0 \leq p_{ij} \leq 1\), valamint \(\sum_i \sum_j p_{ij} = 1\) feltételeknek teljesülniük kell, hogy valóban kétváltozós diszkrét súlyfüggvényről beszélhessünk. A táblázat peremén -- az utolsó sorban és oszlopban -- feltüntettük az ún. peremvalószínűségeket, melyek a két változó szerinti súlyfüggvényeket adják meg.
A peremvalószínűségek egyszerűen a megfelelő sorban, illetve oszlopban található együttes bekövetkezési valószínűségek összegei, azaz \(p_{i.} = \sum_j p_{ij} = \mathbf{P}(X=x_i)\), illetve \(p_{.j} = \sum_i p_{ij} = \mathbf{P}(Y=y_j)\).
Az egyváltozós esethez hasonlóan az eloszlásfüggvény egyszerű felösszegzéssel képezhető, mind a peremeloszlásokra, mind az együttes eloszlásra vonatkozóan. Az \(X\) változó szerinti perem eloszlásfüggvény tehát
\[\begin{equation} F_X(x) = \mathbf{P}(X \leq x) = \sum_{x_i \leq x} \sum_{j} p_{ij} = \sum_{x_i \leq x} p_{i.} \tag{7.2} \end{equation}\]
módon számítható, azaz az együttes bekövetkezési valószínűségek és a peremvalószínűségek összegzésének segítségével is. Az együttes eloszlásfüggvény az egyváltozós eset általánosítása, azt mutatja meg, hogy a valószínűségi vektorváltozó milyen valószínűséggel teljesíti a \(X \leq x\) és \(Y \leq y\) feltételeket:
\[\begin{equation} F_{XY}(x, y) = \sum_{x_i \leq x} \sum_{y_j \leq y} p_{ij} \tag{7.3} \end{equation}\]
| kávé, víz | 0 | 1 | 2 | 3 | összesen |
|---|---|---|---|---|---|
| 0 | \(0{,}1\) | \(0{,}045\) | \(0{,}015\) | \(0{,}015\) | \(0{,}175\) |
| 1 | \(0{,}075\) | \(0{,}15\) | \(0{,}025\) | \(0{,}05\) | \(0{,}3\) |
| 2 | \(0{,}025\) | \(0{,}05\) | \(0{,}125\) | \(0{,}1\) | \(0{,}3\) |
| 3 | \(0\) | \(0{,}025\) | \(0{,}1\) | \(0{,}1\) | \(0{,}225\) |
| összesen | \(0{,}2\) | \(0{,}27\) | \(0{,}265\) | \(0{,}265\) | 1 |
Az együttes bekövetkezési valószínűségek az egyváltozós esethez hasonlóan ábrázolhatók, az egy tengely helyett azonban már kettőre van szükségünk, a lehetséges értékek egy síkon helyezkednek el, a bekövetkezési valószínűségeket pedig a harmadik dimenzióban ábrázoljuk. Három, vagy több valószínűségi változóra vonatkozó súlyfüggvény ábrázolása már nehezen megoldható, mert legalább négy dimenzióra lenne szükség. A 7.1. ábrán a példára vonatkozó kétváltozós súlyfüggvény látható.
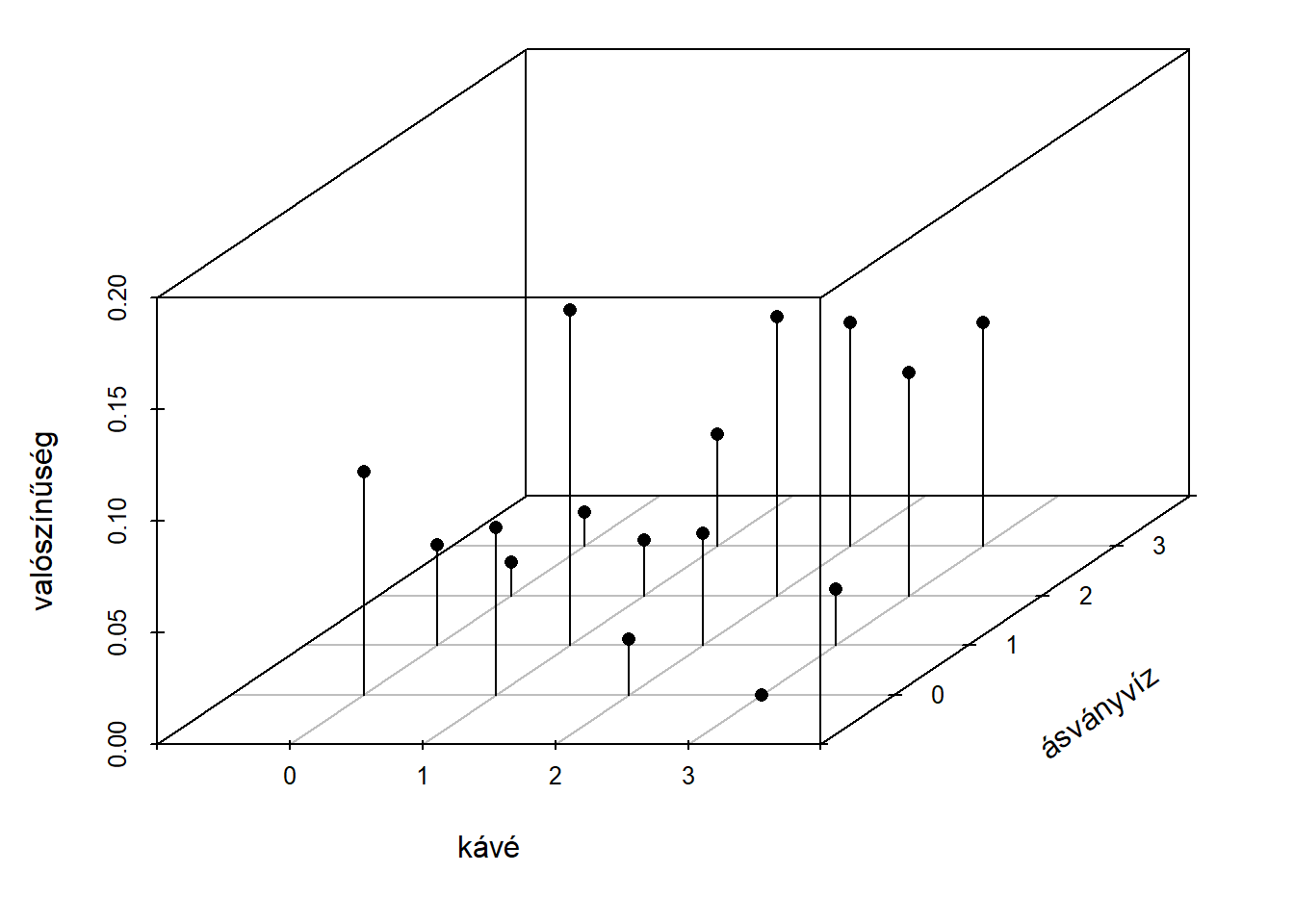
Ábra 7.1: Kétváltozós súlyfüggvény
7.1.2 Feltételes eloszlások
Az, hogy két valószínűségi változót vizsgálunk lehetőséget ad az ún. feltételes eloszlások vizsgálatára is. A feltételes eloszlás alatt azt értjük, hogy az egyik változó fix értéke mellett a másik változó eloszlása hogyan alakul. A feltételes eloszlás vizsgálatához a már korábban tárgyalt, eseményekre vonatkozó feltételes valószínűség fogalmához nyúlunk vissza, amit a (4.9) formulában definiáltunk. A kétváltozós diszkrét eloszlások jelölésrendszerét alkalmazva
\[\begin{equation} \mathbf{P}(X = x_i \mid Y = y_j) = \dfrac{\mathbf{P}(X = x_i, Y = y_j)}{\mathbf{P}(Y = y_j)} = \dfrac{p_{ij}}{p_{.j}} \tag{7.4} \end{equation}\]
amennyiben az \(Y\) változó értéke \(y_j\). Az \(X\) változó értékét rögzítve a feltételes valószínűségek analóg módon határozhatók meg:
\[\begin{equation} \mathbf{P}(Y = y_j \mid X = x_i) = \dfrac{\mathbf{P}(X = x_i, Y = y_j)}{\mathbf{P}(X = x_i)} = \dfrac{p_{ij}}{p_{i.}} \tag{7.5} \end{equation}\]
azaz a feltételes valószínűség kiszámítható az együttes bekövetkezés valószínűségének és a megfelelő peremvalószínűségnek a hányadosaként. Adott feltételhez tartozó valamennyi feltételes valószínűség a feltételes eloszlást adja meg. Mivel az egyik valószínűségi változót adott értéken fixáltuk, így a feltételes eloszlás ebben az esetben egy egyváltozós valószínűségi változó, így az 5. fejezetben megismert elemzési eszközök is alkalmazhatók, így például a feltételes eloszlás várható értéke is kiszámítható, ami a későbbiekben is fontos szerepet kap. Rögzített \(y_j\) esetén a formula
\[\begin{equation} \mathbf{E}(X \mid Y = y_j) = \sum_i x_i \mathbf{P}(X = x_i \mid Y = y_j) = \sum_i x_i \dfrac{p_{ij}}{p_{.j}} \tag{7.6} \end{equation}\]
míg rögzített \(x_i\) esetén
\[\begin{equation} \mathbf{E}(Y \mid X = x_i) = \sum_j y_j \mathbf{P}(Y = y_j \mid X = x_i) = \sum_j y_j \dfrac{p_{ij}}{p_{i.}} \tag{7.7} \end{equation}\]
Tegyük fel, hogy tudjuk, az elmúlt órában \(X = 2\) kávét értékesítettek a benzinkúton, ekkor kíváncsiak lehetünk az egyes ásványvíz értékesítések valószínűségére, valamint a feltételes várható értékre is.
\[ \mathbf{P}(Y = 0 \mid X = 2) = \dfrac{0{,}025}{0{,}3} = \dfrac{1}{12} \quad \mathbf{P}(Y = 1 \mid X = 2) = \dfrac{0{,}05}{0{,}3} = \dfrac{1}{6} \]
\[ \mathbf{P}(Y = 2 \mid X = 2) = \dfrac{0{,}125}{0{,}3} = \dfrac{5}{12} \quad \mathbf{P}(Y = 3 \mid X = 2) = \dfrac{0{,}1}{0{,}3} = \dfrac{1}{3} \]
azaz ha tudjuk, hogy két kávét értékesítettek, akkor annak a valószínűsége, hogy nem értékesítettek ásványvizet mindössze \(\dfrac{1}{12}\), míg a 3 ásványviz valószínűsége \(\dfrac{1}{3}\). Az ezekből számítható feltételes várható érték \(Y\)-ra vonatkozóan pedig a
\[ \mathbf{E}(Y \mid X = 2) = \sum_j y_j \dfrac{p_{ij}}{p_{i.}} = 0 \cdot \dfrac{1}{12} + 1 \cdot \dfrac{1}{6} + 2 \cdot \dfrac{5}{12} + 3 \cdot \dfrac{1}{3} = 2 \]
Azaz ebben a példában, amennyiben tudjuk, hogy egy adott órában két kávét értékesítünk, akkor az eladott ásványvizek várható darabszáma is épp kettő, bár természetesen előfordulhat 0, 1, 2 és 3 is eladott mennyiségként, ahogy azt a feltételes valószínűségek mutatják. A várható érték (hasonlóan az egyváltozós esethez) nem feltétlenül olyan érték, amely lehetséges, így például
\[ \mathbf{E}(Y \mid X = 3) = 2{,}333 \]
Adott mennyiségű ásványvízhez tartozó kávéra vonatkozó valószínűségek és várható értékek analóg módon számíthatók.
A feltételes várható érték mellett a feltételes eloszlás varianciája, vagy bármilyen egyéb momentuma is meghatározható, az egyváltozós esettel analóg módon, ez azonban meghaladja tananyagunk kereteit.
7.1.3 Függetlenség
Két esemény függetlenségét a (4.12) formulával, a 4.3. fejezetben definiáltuk, két valószínűségi változó függetlensége támaszkodik ezekre az ismeretekre. Azt mondjuk, hogy \(X\) és \(Y\) valószínűségi változó független, ha
\[\begin{equation} \mathbf{P}(X = x_i \mid Y = y_j) = \mathbf{P}(X = x_i) \tag{7.8} \end{equation}\]
minden \(i\) és \(j\) esetén teljesül, azaz bármilyen, \(Y\)-ra vonatkozó információ sem változtatja meg az \(x_i\) események valószínűségét. A definíció fordítottja is kimondható, azaz függetlenség esetén
\[\begin{equation} \mathbf{P}(Y = y_j \mid X = x_i) = \mathbf{P}(Y = y_j) \tag{7.9} \end{equation}\]
Ez pontosan akkor teljesül, ha
\[\begin{equation} \mathbf{P}(X = x_i, Y = y_j) = \mathbf{P}(X = x_i) \mathbf{P}(Y = y_j) \tag{7.10} \end{equation}\]
minden \(i\) és \(j\) esetén teljesül, azaz az együttes bekövetkezési valószínűségek a teljes táblázatban a hozzájuk tartozó peremvalószínűségek szorzataiként előállíthatók.
A példánkban szereplő \(X\) és \(Y\) valószínűségi változók nem függetlenek, hiszen már korábban láttuk, hogy pl.
\[ \mathbf{P}(Y = 0 \mid X = 2) = \dfrac{1}{12} \neq \mathbf{P}(Y = 0) = 0{,}2 \]
Mivel az azonosságnak minden feltételes valószínűségre teljesülni kell függetlenség esetén, ezért már egy ellenpélda esetén is kimondhatjuk, hogy a valószínűségi változók nem függetlenek. Egyezőség esetén azonban tovább kell vizsgálódnunk, hogy minden esetben fennáll-e az.
A függetlenség ellenőrizhető a (7.10) egyenlet alapján is, amihez -- és később megismerendő vizsgálatokhoz -- érdemes elkészíteni a függetlenség esetén érvényes valószínűségeket a peremvalószínűségek segítségével. A példánk esetén ez három tizedesre kerekítve az alábbi táblázatban látható.
| kávé, víz | 0 | 1 | 2 | 3 | összesen |
|---|---|---|---|---|---|
| 0 | \(0{,}035\) | \(0{,}047\) | \(0{,}046\) | \(0{,}046\) | \(0{,}175\) |
| 1 | \(0{,}060\) | \(0{,}081\) | \(0{,}080\) | \(0{,}080\) | \(0{,}3\) |
| 2 | \(0{,}060\) | \(0{,}081\) | \(0{,}080\) | \(0{,}080\) | \(0{,}3\) |
| 3 | \(0{,}045\) | \(0{,}061\) | \(0{,}060\) | \(0{,}060\) | \(0{,}225\) |
| összesen | \(0{,}2\) | \(0{,}27\) | \(0{,}265\) | \(0{,}265\) | 1 |
7.1.4 Vektorváltozó momentumai
Az egyváltozós eloszlások legfontosabb momentumai (5.2. és 6.2. fejezetek) a várható érték és a variancia. Vektorváltozó esetén a várható érték szerepét skalár helyett egy vektor, míg a variancia szerepét egy mátrix veszi át.
Kétváltozós diszkrét eloszlás esetében a várható érték egy kétdimenziós vektor
\[\begin{equation} \mathbf{E} \left[\begin{array}{c} X \\ Y \end{array}\right]= \left[\begin{array}{c} \sum_{i}x_i p_{i\cdot} \\ \sum_{j}y_j p_{\cdot j} \end{array}\right] \tag{7.11} \end{equation}\]
azaz a várható érték vektor egyszerűen a komponensek várható értékeinek felsorolásából áll, amiből következik, hogy az egyváltozós esetnél megfigyelt tulajdonságok öröklődnek.
Az egyváltozós esetben megismert variancia helyét a \(\mathbf{C}\) variancia-kovariancia mátrix veszi át, amely kétváltozós esetben \(2 \times 2\)-es:
\[\begin{equation} \mathbf{C}=\left[\begin{array}{cc}\mathbf{D}^2(X) & \mathrm{Cov}(X,Y) \\ \mathrm{Cov}(Y,X) & \mathbf{D}^2(Y)\end{array}\right] \tag{7.12} \end{equation}\]
amiben a két változó varianciáját mérő \(\mathbf{D}^2(X)\) és \(\mathbf{D}^2(Y)\) mellett a két változó együttmozgását mérő kovariancia is megjelenik, amely szimmetrikus, azaz \(\mathrm{Cov}(X,Y)=\mathrm{Cov}(Y,X)\). A kovariancia az alábbi módon számítható
\[\begin{equation} \mathrm{Cov}(X,Y)=\mathbf{E}\big( (X-\mathbf{E}(X))(Y-\mathbf{E}(Y)) \big)=\mathbf{E}(XY)-\mathbf{E}(X)\cdot\mathbf{E}(Y) \tag{7.13} \end{equation}\]
ami diszkért esetben a
\[\begin{equation} \mathrm{Cov}(X,Y)=\sum_i\sum_j x_iy_jp_{ij}-\left(\sum_ix_ip_{i\cdot}\right)\left(\sum_jy_jp_{\cdot j}\right) \tag{7.14} \end{equation}\]
formában írható fel. A szimmetria mellett a kovariancia alábbi fő tulajdonságait említjük meg:
- bármely valószínűségi változó konstanssal vett kovarianciája 0, azaz \(\mathrm{Cov}(X,a) = 0\)
- lineáris transzformációk esetén \(\mathrm{Cov}(aX+b,cY+d) = ac\mathrm{Cov}(X,Y)\)
- a variancia tulajdonképp egy valószínűségi változó önmagával vett kovarianciája \(\mathrm{Cov}(X,X) = \mathbf{D}^2(X)\)
A példánkban a várható érték vektor a két (feltétel nélküli) várható értéket tartalmazza \[ \mathbf{E} \left[\begin{array}{c} X \\ Y \end{array}\right]= \left[\begin{array}{c} 0 \cdot 0{,}175 + 1 \cdot 0{,}3 + 2 \cdot 0{,}3 + 3 \cdot 0{,}225\\ 0 \cdot 0{,}2 + 1 \cdot 0{,}27 + 2 \cdot 0{,}265 + 3 \cdot 0{,}265 \end{array}\right] = \left[\begin{array}{c} 1{,}575 \\ 1{,}595 \end{array}\right] \]
A variancia-kovariancia mátrix elemei közül a kovariancia kiszámítását szemléltetjük, elsőként számítsuk ki a \(\mathbf{E}(XY)\) várható értéket.
\[ \mathbf{C}=\left[\begin{array}{cc}\mathbf{D}^2(X) & \mathrm{Cov}(X,Y) \\ \mathrm{Cov}(Y,X) & \mathbf{D}^2(Y)\end{array}\right]=\left[\begin{array}{cc}1{,}044375 & 0{,}612875 \\ 0{,}612875 & 1{,}170975\end{array}\right] \]
\[\begin{equation*} \begin{split} \mathbf{E}(XY) & = \sum_i\sum_j x_iy_jp_{ij} = \\ & =0 \cdot 0 \cdot 0{,}1 + \dots + 1 \cdot 0 \cdot 0{,}075 + 1 \cdot 1 \cdot 0{,}15 + \dots + 3 \cdot 3 \cdot 0{,}1 = 3{,}125 \end{split} \end{equation*}\]
amiből a kovariancia egyszerűen adódik:
\[ \mathrm{Cov}(X,Y)=\mathbf{E}(XY)-\mathbf{E}(X)\cdot\mathbf{E}(Y) = 3{,}125 - 1{,}595 \cdot 1{,}575 = 0{,}612875 \]
A kovariancia tehát pozitív, ami azt jelenti, hogy az egyik változó nagyobb értékei a másik változó nagyobb értékeivel fordulnak elő együtt gyakran, illetve a kis értékek is gyakran járnak együtt. Ezt fogalmaztuk meg már korábban, a súlyfüggvény vizsgálatakor is úgy, hogy a kávé és az ásványvíz ezen a benzinkúton kiegészítő termékek. Helyettesítő termékek esetén a kovariancia negatív értéket venne fel.
Az egyváltozós diszkrét valószínűségi változókkal analóg módon kiszámított varianciák és a kovariancia alapján felírható tehát a variancia-kovariancia mátrix: \[ \mathbf{C}=\left[\begin{array}{cc}\mathbf{D}^2(X) & \mathrm{Cov}(X,Y) \\ \mathrm{Cov}(Y,X) & \mathbf{D}^2(Y)\end{array}\right]=\left[\begin{array}{cc}1{,}044375 & 0{,}612875 \\ 0{,}612875 & 1{,}170975\end{array}\right] \]7.1.5 Korreláció
A kovariancia tehát két valószínűségi változó együttmozgásának mértékét méri, hátránya azonban, hogy függ a változók nagyságrendjétől. Ahogyan azt láttuk, ha az \(X\) változót \(a\)-szorosára változtatjuk, a kovariancia is \(a\)-szorosára változik, annak ellenére, hogy ez nem jelenti azt, hogy az \(Y\) változóval való együttmozgása megváltozott. Ha például \(X\) költséget, vagy profitot jelöl, és forint helyett 1000 forintban mérjük, a kovariancia 0,001-szeresére változna. Ezt a tulajdonságot hivatott kiküszöbölni egy nagyon gyakran alkalmazott mérőszám, a korreláció.
Két valószínűségi változó közötti kapcsolat szorosságát és irányát a
\[\begin{equation} \rho(X,Y)=\frac{\mathrm{Cov}(X,Y)}{\sqrt{\mathbf{D}^2(X)\cdot\mathbf{D}^2(Y)}} \tag{7.15} \end{equation}\]
ún. lineáris korrelációs együtthatóval mérjük. Legfontosabb tulajdonságai:
- szimmetrikus, azaz \(\rho(X,Y) = \rho(Y,X)\),
- \(-1 \leq \rho(X,Y) \leq 1\),
- az előjel a kapcsolat irányát jelöli,
- \(\rho(X,Y) = 0\) neve korrelálatlanság,
- \(|\rho(X,Y)| = 1\) neve függvényszerű lineáris kapcsolat, tökéletes negatív, vagy pozitív lineáris korreláltság.
Általánosságban minél közelebb van a korrelációs együttható abszolút értéke 1-hez, annál erősebb korrelációs kapcsolatról beszélünk a két valószínűségi változó között.
Amint azt láttuk, a kovariancia értéke pozitív a példánkban, előjele igen, nagysága nem értelmezhető önmagában. A kovarianciából számított korrelációs együttható azonban biztosan \(-1\) és \(1\) közötti értéket vesz fel. \[ \rho(X,Y)=\frac{\mathrm{Cov}(X,Y)}{\sqrt{\mathbf{D}^2(X)\cdot\mathbf{D}^2(Y)}} = =\frac{0{,}612875}{\sqrt{1{,}044375 \cdot 1{,}170975}} = 0{,}5542 \]
Azaz a korrelációs együttható -- a kovarianciával szükségszerűen azonos -- pozitív előjelű, azaz pozitív, de nem tökéletes lineáris korrelációt tapasztalunk a két valószínűségi változó között.Gyakran keveredik össze a 7.1.3. fejezetben tárgyalt függetlenség, valamint a korrelálatlanság fogalma, ezért ezen a helyen néhány szót ejtünk a két fogalom közötti kapcsolatról
- bizonyítható, hogy ha \(X\) és \(Y\) függetlenek, akkor korrelálatlanok, azaz \(\rho(X,Y) = 0\)
- a korrelálatlanság azonban nem jelenti egyben azt, hogy a valószínűségi változók függetlenek!
Ilyen értelemben a két valószínűségi változó közötti függetlenség erősebb állítás, mint a korrelálatlanság. A 0 korrelációs együttható csak annyit jelent, hogy lineáris összefüggés nem figyelhető meg a váltózók között, de más, pl. parabolaszerű kapcsolat elképzelhető.
Legyen \(X\) és \(Y\) együttes eloszlása az alábbi
| X, Y | -1 | 0 | 1 |
|---|---|---|---|
| 0 | \(0\) | \(0{,}5\) | \(0\) |
| 1 | \(0{,}25\) | \(0\) | \(0{,}25\) |