8.2 Mintavételi eloszlások
Az üzleti életben és más, statisztikai módszereket alkalmazó területeken is gyakran előfordul, hogy nem ismerjük a teljes sokaságot, így minta alapján kell döntéseket hoznunk. A következtetéses statisztika egyik nagy területe a becslés, melynek során egy sokasági paraméter közelítő értékét kívánjuk meghatározni egy mintabeli statisztika segítségével. A statisztikai becslés elvégzéséhez azonban elsőként azt kell megértenünk, hogy egy adott sokaságból kiválasztható összes minta hogy viselkedik. Becslést bármelyik, a 2. és 3. fejezetekben megismert sokasági paraméterre vonatkozóan készíthetnénk, de jelen tananyagunkban elsősorban két gyakran vizsgált paraméterre, a sokasági átlagra és a sokasági arányra koncentrálunk. A gyakorlatban tehát egyetlen minta átlaga alapján fogunk következtetéseket levonni a sokasági átlagra vonatkozóan, illetve egyetlen mintában tapasztalt arány alapján következtetünk a sokasági arányra. Ahhoz, hogy ezt el tudjuk végezni, először végiggondoljuk, hogy adott sokaságból milyen lehetséges mintaátlagú minták, illetve milyen mintabeli aránnyal rendelkező minták keletkezhetnek. Az összes lehetséges minta alapján kiszámított átlagokat (melyek különbözők lesznek) az átlag mintavételi eloszlásának, analóg módon az arányokat az arány mintavételi eloszlásának nevezzük. Természetesen az összes többi paraméter (medián, szórás, variancia, kvartilisek, stb.) is rendelkezik mintavételi eloszlással, ezekről azonban részletesen nem beszélünk.
Mivel a következtetéses statisztika területére lépünk, át kell ismételnünk a már alkalmazott jelöléseket, illetve újakat is be kell vezetnünk:
- \(N, n, \frac{n}{N}\): rendre alapsokaság elemszáma, minta elemszáma és kiválasztási arány,
- \(\mu, \sigma, \pi\): rendre alapsokasági átlag, szórás és arány,
- \(\overline{X}, S, P\): rendre a mintabeli átlag, szórás és arány valószínűségi változója,
- \(\overline{x}, s, p\): rendre a mintabeli átlag, szórás és arány egy adott mintából számított realizációja, amit a gyakorlatban megfigyelhetünk.
Fontos továbbá, hogy valamennyi mintaelem valószínűségi változó, azaz őket általánosan \(X_i\)-vel fogjuk jelölni.3 A mintalemek tehát valószínűségi változók, mivel -- a mintavétel előtt -- értékük ismeretlen, a mintaelemek realizációját \(x_i\)-vel fogjuk jelölni \((i = 1,2, \dots, n)\). Az \(X_i = x_i\) esemény tehát azt jelenti, hogy az \(i\). mintaelem épp \(x_i\) értéket vesz fel, hasonlóan a diszkrét és folytonos valószínűségi változóknál alkalmazott jelöléshez. Az általános mintaelem eloszlása megegyezik a sokaság eloszlásával, így \(\mathbf{E}(X_i) = \mu\), valamint \(\mathbf{D}^2(X_i) = \sigma^2\)
8.2.1 Az átlag mintavételi eloszlása
Az átlag mintavételi eloszlásának vizsgálatát egy egyszerű példán keresztül vezetjük be, levonunk néhány következtetést, majd innen haladunk az összetettebb esetek felé.
Legyenek egy \(N=4\) elemű sokaság, elemei 33, 36, 49 és 62 (életkorok évben). Könnyen kiszámíthatjuk, hogy ekkor az átlagéletkor \(\mu = 45\) év és \(\sigma = 11{,}51\) év a sokasági szórás. Vizsgáljuk meg az összes \(n = 2\) elemű visszatevéssel húzott mintát. Mivel csupán 16 különböző lehetséges minta van, ezeket fel tudjuk sorolni, majd valamennyi esetben meg tudjuk határozni a mintaátlag adott mintára érvényes realizációját. Ezeket a 8.1. táblázat tartalmazza.
| # | \(x_1\) | \(x_2\) | \(\overline{x}\) | # | \(x_1\) | \(x_2\) | \(\overline{x}\) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 33 | 33 | 33,0 | 9 | 49 | 33 | 41,0 | |
| 2 | 33 | 36 | 34,5 | 10 | 49 | 36 | 42,5 | |
| 3 | 33 | 49 | 41,0 | 11 | 49 | 49 | 49,0 | |
| 4 | 33 | 62 | 47,5 | 12 | 49 | 62 | 55,5 | |
| 5 | 36 | 33 | 34,5 | 13 | 62 | 33 | 47,5 | |
| 6 | 36 | 36 | 36,0 | 14 | 62 | 36 | 49,0 | |
| 7 | 36 | 49 | 42,5 | 15 | 62 | 49 | 55,5 | |
| 8 | 36 | 62 | 49,0 | 16 | 62 | 62 | 62,0 |
A fenti példára vonatkozóan a következő megállapításokat tehetjük:
- egyik mintaátlag sem "találja el" a sokasági átlagot, de jellemzően közel esnek a \(\mu = 45\) értékhez
- a mintaátlagok átlaga (jelöljük \(\mathbf{E}(\overline{X}) = \mu_{\overline{X}}\) módon) épp a sokasági átlaggal egyezik meg, hiszen (a számításnál azt is felhasználtuk, hogy a különböző minták bekövetkezési valószínűsége egyenlő, így nincs szükség súlyozásra) \[ \mu_{\overline{X}} = \dfrac{33 + 34{,}5 + \dots + 62}{16} = 45 \]
- a mintaátlagok szórása (jelöljük \(\mathbf{D}(\overline{X}) = \sigma_{\overline{X}}\) módon) a sokasági szórásnál kisebb, hiszen \[ \sigma_{\overline{X}} = \sqrt{\dfrac{(33 - 45)^2 + (34{,}5 - 45)^2 + \dots + (62 - 45)^2}{16}} = 8{,}14 \]
A fenti példában azt tapasztaltuk, hogy az összes visszatevéssel vett mintaátlag várható értéke pontosan megegyezik a sokasági átlaggal. Az átlag ezen könnyen belátható tulajdonságát torzítatlanságnak nevezzük, amely természetesen nem csak a fenti példában állja meg a helyét. Tudjuk tehát, hogy ugyan valószínűleg az aktuálisan kiválasztott mintánk átlaga nem egyezik meg pontosan a keresett \(\mu\) sokasági paraméterrel, de az összes kiválasztható minta esetén az egyezőség várható értékben teljesül, azaz
\[\begin{equation} \mu_{\overline{X}} = \mu \tag{8.1} \end{equation}\]
A következő felismerésünk talán még fontosabb, hiszen pontosan arra vagyunk kíváncsiak, hogy az egyes lehetséges mintaátlagok milyen távol esnek a valós sokasági átlagtól. A mintaátlagok szórása pedig épp ezt mutatja meg, hiszen a szórás definíciója alapján az egyes egyedek átlagtól vett átlagos távolságát mutatja meg. Jelen esetben az egyedek az egyes lehetséges mintaátlagok, a mintaátlagok átlagáról pedig tudjuk, hogy az épp a sokasági átlag (lásd torzítatlanság). A mintaátlagok szórását az átlag standard hibájának nevezzük, ami épp a mintavétel átlagos hibáját mutatja meg.
A standard hiba \(n\) elemű, független azonos eloszlású mintavétel esetén, kihasználva, hogy az egyes mintaelemek varianciája azonos
\[\begin{equation} \sigma_{\overline{X}} = \frac{\sigma}{\sqrt{n}} \tag{8.2} \end{equation}\]
azaz azt látjuk, hogy a standard hiba (a mintavétel által okozott átlagos hiba, az abból eredő átlagos hiba, hogy nem figyeljük meg a teljes sokaságot) egyrészt függ a sokaság heterogenitásától, másrészt a minta méretétől. Minél nagyobb a sokasági szórás, annál heterogénebbek a lehetséges mintaátlagok is, illetve ami talán még fontosabb: a mintaelemszám növelésével az adott sokaságból levonható következtetéseink egyre pontosabbak lesznek.
Az előző példa adatai alapján ellenőrizhető, hogy az összefüggés valóban teljesül-e \[ \sigma_{\overline{X}} = \frac{\sigma}{\sqrt{n}} = \frac{11{,}51}{\sqrt{2}} = 8{,}14 \] azaz ugyanazt az eredményt kaptuk pusztán a sokasági szórás és a mintaelemszám felhasználásával, mint az összes mintaátlag szórásának kiszámításával. A standard hiba tehát azt jelenti ebben az esetben, hogy átlagosan 8,14 évvel térnek el a mintaátlagok a saját átlaguktól, azaz a sokasági átlagtól. Átlagosan 8,14 évet tévedünk, ha egy kételemű minta alapján becsüljük meg a sokasági életkort.
Természetesen nagyobb \(N\) és \(n\) esetén az összes mintaátlag meghatározása már nem járható út, de a (8.1) és (8.2) összefüggések természetesen továbbra is érvényesek. Ezek az azonosságok megadják a mintavételi eloszlás várható értékét és szórását, azonban arra nem adnak választ, hogy milyen az eloszlás típusa.
Amennyiben a sokaság normális eloszlású, belátható, hogy a mintavételi eloszlás is normális eloszlást követ és a (8.1), (8.2) összefüggések miatt a különböző \(n\)-ek esetére érvényes mintavételi eloszlások várható értéke \(\mu\), szórása pedig egyre kisebb, hiszen \(\sigma\)-t egyre nagyobb \(\sqrt{n}\) nevezővel kell osztanunk. Ez azt jelenti, hogy egyre nagyobb minták esetén a mintaátlagok egyre inkább a sokasági átlag körül tömörülnek. Mivel a mintavételi eloszlás normális, ezért olyan kérdésekre is választ tudunk adni, hogy mi a valószínűsége, hogy egy adott sokaságból \(n\) elemű mintát véve a mintaátlag adott intervallumba esik.
Legyen \(X \sim \mathcal{N}(100, 15)\), ami az IQ eloszlását jól leírja a sokaságban. Számítsuk ki az alábbi valószínűségeket:
- egy véletlenül kiválasztott egyén IQ-ja 90 és 110 között van \[ \mathbf{P}(90 < X < 110) = 0{,}495 \]
- öt véletlenül kiválasztott egyén átlagos IQ-ja 90 és 110 között van \[ \mathbf{P}(90 < \overline{X} < 110) = 0{,}864 \]
- tizenöt véletlenül kiválasztott egyén átlagos IQ-ja 90 és 110 között van \[ \mathbf{P}(90 < \overline{X} < 110) = 0{,}990 \]
A legtöbb gyakorlati esetben azonban a sokaság ismeretlen eloszlású, illetve a sokaság normalitását nem is tételezhetjük fel. Ebben az esetben a mintavételi eloszlás alakjának meghatározása összetett feladat. A Centrális Határeloszlás-Tétel (CHT), vagy központi határeloszlás-tétel azonban kimondja, hogy elégségesen nagy számú független mintavétel esetén a mintavételi eloszlás közelítőleg normálissá válik.4 Természetesen az elégségesen nagy minta méretének meghatározása sem egyszerű, az függ a sokaság alakjától, de a különböző tankönyvek \(n=30\) és \(n=100\) közötti általános határértékről beszélnek. Természetesen léteznek olyan extrém eloszlások, melyek esetén akár a több ezer elemű minták mintavételi eloszlása sem közelíthető jól a normális eloszlással, ezek tárgyalása azonban meghaladja tananyagunk kereteit.
A 8.1. ábrán öt különböző sokasági eloszlásból vett véletlen minták mintaátlagainak eloszlását tüntettük fel. A sokaságok sűrűségfüggvényei a felső sorban láthatók, a szaggatott vonalak az eloszlások várható értékét mutatják. A következő sorokban egyre nagyobb minta alapján rajzoltuk meg a mintavételi eloszlást, valamint a mintavételi eloszlás várható értékét.5
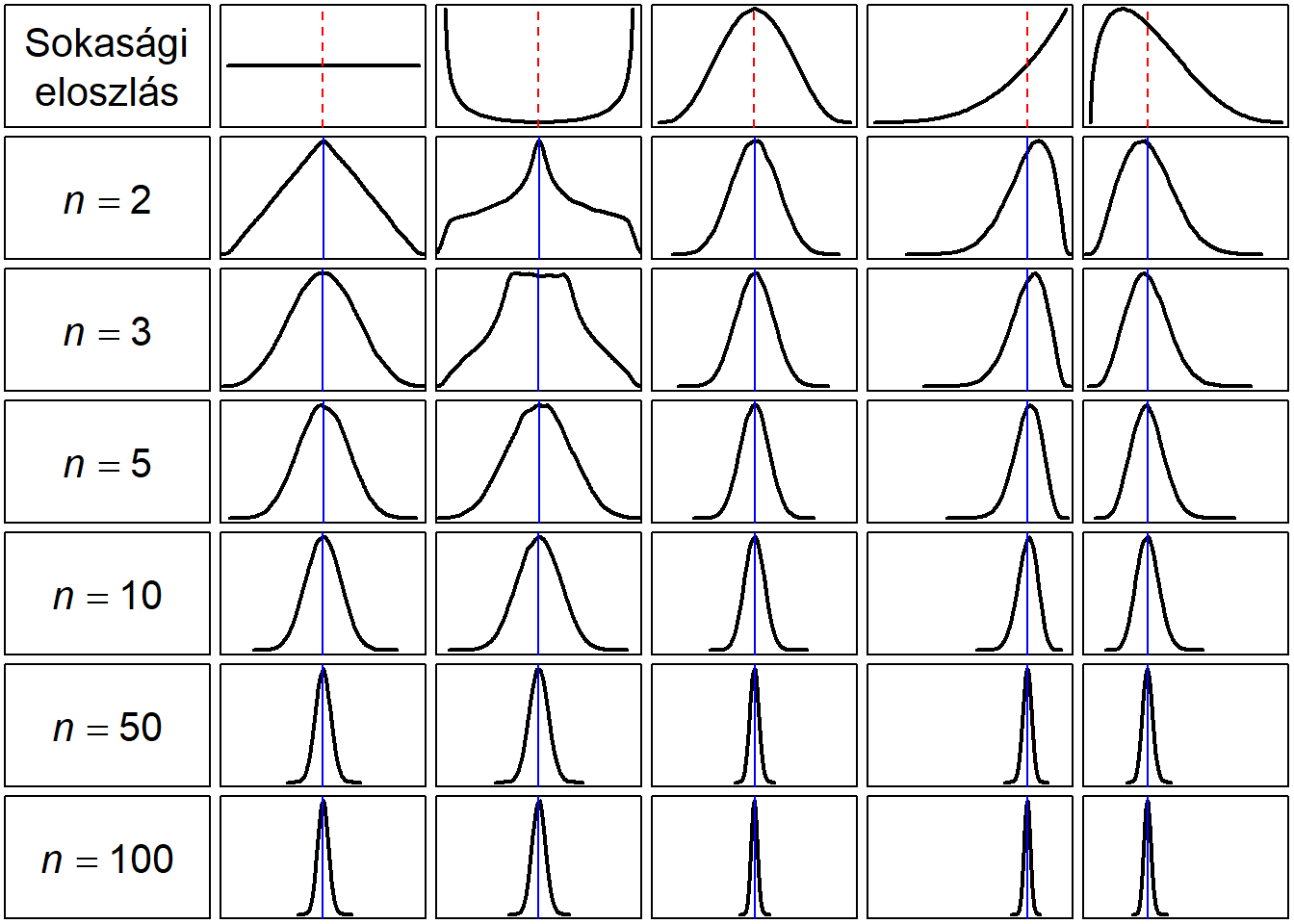
Ábra 8.1: A CHT működése öt különböző sokaság esetén
A 8.1. ábra alapján levonható következtetések
- a mintavételi eloszlások várható értéke minden esetben megegyezik a sokasági átlaggal
- a mintavételi eloszlások szórása a minta nagyságának növekedésével csökken
- a mintavételi eloszlások a minta nagyságának növekedésével egyre inkább hasonlítanak a normális eloszlásra
A Centrális határeloszlás-tétel szerint tehát ha \(X_1, X_2, \dots, X_n\) független, azonos eloszlású véletlen változók \(\mu\) várható értékkel és \(\sigma^2\) varianciával, akkor
\[\begin{equation} \lim_{n\to\infty}\frac{X_1+X_2+\dots +X_n}{n}=\overline{X}\sim\mathcal{N}\left(\mu_{\overline{X}},\sigma_{\overline{X}}\right), \tag{8.3} \end{equation}\] ahol \(\overline{X}\) a mintaátlag valószínűségi változója, melynek várható értéke \(\mu_{\overline{X}}=\mu\), szórása pedig \(\sigma_{\overline{X}}=\sigma/\sqrt{n}\).
Ahogy azt már a 6.3.3. fejezetben is láttuk, gyakran a standard normális eloszlás használata a kézenfekvőbb, a következtetéses statisztika sok területe is ezt használja. A fenti állítás standardizálás után úgy is megfogalmazható, hogy elegendően nagy minta esetén
\[\begin{equation} Z = \dfrac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}} \sim \mathcal{N}\left(0,1\right) \tag{8.4} \end{equation}\]
ami a következtetéses statisztika egyik legfontosabb összefüggése, segítségével valószínűségi állításokat tehetünk a mintaátlaggal kapcsolatosan.
Amennyiben a mintavétel nem függetlenül történik, azaz egyszerű véletlen mintavételről beszélünk (véges alapsokaságból, visszatevés nélküli minta), akkor bizonyítható, hogy a standard hiba megváltozik
\[\begin{equation} \sigma_{\overline{X}}=\frac{\sigma}{\sqrt{n}}\sqrt{\frac{N-n}{N-1}} \tag{8.5} \end{equation}\] ahol a második tényező neve véges szorzó, utalva arra, hogy véges alapsokaságból választottuk a mintát. Ezzel kapcsolatban az alábbi megállapításokat tehetjük:
- A véges szorzó csökkenti a mintaátlag bizonytalanságát, hiszen értéke 1 alatti.
- \(n \to N\) esetben \(\sigma_{\overline{X}} \to 0\), azaz ha a minta mérete megközelíti a sokaság méretét, akkor a bizonytalanság 0-hoz tart.
- \(N \to \infty\) esetben a véges szorzó hatása jelentéktelen, végtelen nagy (a gyakorlatban nagy) sokaságok esetén használatától eltekinthetünk.
- Gyakran közelítjük az egyszerűbb \(\sqrt{1-\frac{n}{N}}\) formulával, ami némileg beszédesebb: minél nagyobb a mintavételi arány, annál inkább csökkenthető a standard hiba. Nagyon kicsi, néhány százalékos mintavételi arány esetén a tényező értéke közel egy, így érdemben nem befolyásolja a véges szorzó a standard hibát.
- A binomiális és hipergeometriai eloszlások varianciái épp ebben a véges szorzóban különböznek, lásd (5.12) és (5.14).
Legyen a vizsgált sokaságunk mérete \(N = 10\,000\). Amennyiben \(n = 100\) elemű a mintánk, azaz a \(n/N\) kiválasztási arány 1%-os, a véges szorzó értéke \[ \sqrt{\frac{N-n}{N-1}} = 0{,}99504 \] azaz a hibahatár mindössze fél százalékkal csökken, a közelítő képletet alkalmazva pedig 0,99499 értéket kapunk. A gyakorlatban ezek az értékek elhanyagolhatóan kicsik. Abban az esetben azonban, ha a sokaság mérete mindössze \(N = 500\), a véges szorzó értéke 0,895 körül alakul.
8.2.2 Az arány mintavételi eloszlása
Sok esetben nem a sokasági átlagra, hanem a korábban6 \(\pi\)-vel jelölt, adott tulajdonsággal rendelkező egyedek sokasági arányára szeretnénk következtetéseket levonni. A sokasági arányra vonatkozó következtetésekben a mintabeli arány lesz segítségünkre, így a mintabeli arány mintavételi eloszlását is meg kell ismernünk. Jelölje \(P\) a mintabeli arány valószínűségi változóját, \(p\) pedig a mintabeli arány egy realizációját. Belátható, hogy független mintavételezés esetén a mintabeli arány is torzítatlan és normális eloszlást követ, méghozzá
\[\begin{equation} P \sim \mathcal{N}(\pi,\sigma_P) \tag{8.6} \end{equation}\] paraméterekkel, ahol \(\sigma_P=\sqrt{\dfrac{\pi(1-\pi)}{n}}\) az arány standard hibája. A normális eloszlással történő közelítés abban az esetben alkalmazható, ha a mintaelemszám elegendően nagy. A legtöbb tankönyv feltételként azt követeli meg, hogy \(n\pi>5\) és \(n(1-\pi)>5\) is teljesüljenek, néhol a szigorúbb \(n\pi>10\) és \(n(1-\pi)>10\), vagy az \(n\pi(1-\pi)>5\) feltételeket adják meg. Valamennyi feltétel tartalma azonos: amennyiben \(\pi\) közel 0,5, elegendő viszonylag kis, 10-20 elemű minta a normalitáshoz, míg a 0,5 értéktől távolodva egyre nagyobb mintára van ehhez szükség. Más megközelítésben a normális közelítés megfelelő, ha a keresett arány se nem túl kicsi, se nem túl nagy a mintaelemszámhoz képest.
Mindez azt jelenti, hogy egy \(\pi\) sokasági aránnyal jellemezhető sokaságból minden \(n\) elemű mintát kiválasztva a \(p\) mintabeli arányok átlaga pontosan \(\pi\), valamint a mintaelemszám növekedésével a mintabeli arányok egyre inkább megközelítik a sokasági arányt.
Abban az esetben, ha a mintát visszatevés nélkül vesszük és a sokaság viszonylag kicsi, az átlag standard hibája esetén megismert véges szorzó alkalmazható:
\[\begin{equation} \sigma_P=\sqrt{\dfrac{\pi(1-\pi)}{n}}\sqrt{\frac{N-n}{N-1}} \tag{8.7} \end{equation}\]
Tegyük fel, hogy egy párt támogatottsága a választók teljes körében \(\pi = 0{,}2\), azaz 20%. Amennyiben \(n = 100\) elemű mintát választunk, mit mondhatunk el a lehetséges mintabeli arányokról? Mi a valószínűsége, hogy az egyetlen kiválasztott mintában a mintabeli arány 25% feletti lesz? Hogyan változik a tudásunk, ha tudjuk, hogy \(N = 500\) és a mintát visszatevés nélkül választjuk?
Mivel \(n\pi = 20\) és \(n(1-\pi) = 80\), ezért a mintavételi eloszlás normalitása feltételezhető, azaz (8.6) alapján tudjuk, hogy a lehetséges mintabeli arányok \(P \sim \mathcal{N}(0{,}2, 0{,}04)\) normális eloszlást követnek. A 6.3.3. fejezetben tanultak alapján pedig \[ \mathbf{P}(P > 0{,}25) = 0{,}1056 \] annak a valószínűsége, hogy egy véletlenül választott \(n = 100\) elemű mintában a mintabeli arány 25% feletti, feltéve hogy \(\pi = 0{,}2\)
Amennyiben véges sokaságból visszatevés nélkül választjuk a mintát, úgy a standard hiba a véges szorzóval módosul, azaz \(P \sim \mathcal{N}(0{,}2, 0{,}0358)\). Az azonos módon számított valószínűség \(\mathbf{P}(P > 0{,}25) = 0{,}0813\), tehát csökkent a valószínűsége, hogy viszonylag nagy tévedést követünk el.8.2.3 A variancia mintavételi eloszlása
A mintaátlag és a mintabeli arány mintavételi eloszlásának megismerése után foglalkozzunk röviden a mintabeli variancia eloszlásával. Gyakran ugyanis nem csak az a fontos, hogy a termékünk átlagosan megfelelő legyen, hanem ezt a magas minőséget alacsony varianciával is kell előállítanunk, hiszen az egyedi vásárlóinkat nem az átlagos termék, hanem az az egyetlen termék érdekli, amit megvásárolt.
A variancia esetén a vizsgálandó valószínűségi változó meghatározása nem annyira magától értetődő, mint az átlag és az arány esetén (ahol a sokasági paramétert az azonosan képzett mintabeli statisztikával vizsgáltuk). Tekintsük a
\[\begin{equation} S^2 = \frac{\sum_{i=1}^n \left(X_i - \overline{X} \right)^2}{n-1} \tag{8.8} \end{equation}\] valószínűségi változót, ahol a szokásos jelölések mellett \(S^2\) jelöli a mintabeli korrigált variancia, így \(S\) a mintabeli korrigált szórás valószínűségi változóját. Első ránézésre a formula hasonlít a (2.13) képletre, azzal a különbséggel, hogy \(N\) helyett \(n\) négyzetösszeget adunk össze, valamint a sokasági átlag helyett a mintaátlag szerepel. Különbség ugyanakkor az is, hogy a nevezőben \(n-1\) szerepel a "várt" \(n\) helyett. Ennek az az oka, hogy ugyan \(n\) független mintaelemet veszünk, azonban miután már ismerjük a mintaátlag értékét, ebből csak \(n-1\) darab határozható meg szabadon. A jelenséget szabadságfoknak nevezi a statisztika. A mintabeli varianciát azért számoljuk így, mert ebben az esetben igaz, hogy
\[\begin{equation} \mathbf{E}(S^2) = \sigma^2 \tag{8.9} \end{equation}\]
Azt már tudjuk tehát, hogy a mintabeli variancia várható értéke a sokasági variancia, és ez az eredmény viszonylag általános, azonban a mintavételi eloszlását még nem ismerjük. Amennyiben a sokaság eloszlása normális, a mintavételi eloszlásnak egy -- eddig ismeretlen -- nevezetes eloszláshoz van köze, ami a \(\chi^2\) eloszlás7. Legyen tehát \(X\) egy normális eloszlású sokaság, ismert \(\sigma^2\) varianciával, ekkor
\[\begin{equation} \frac{\left( n-1 \right) S^2}{\sigma^2} \sim {}_{n-1}\chi^2 \tag{8.10} \end{equation}\] azaz \(n-1\) szabadságfokú \(\chi^2\) eloszlást követ. A \(\chi^2\) eloszlást egyetlen paraméter, a szabadságfok segítséggel határozzuk meg. Az \(n-1\) szabadságfokú \(\chi^2\) eloszlás egyébként \(n-1\) darab, egymástól független standard normális eloszlású véletlen változó négyzetösszegeként állítható elő.
A mintabeli átlag és arány mintavételi eloszlása -- ahogy láttuk, bizonyos feltételek mellett -- a normális eloszláshoz kötődik, a variancia esetén azonban a csak pozitív értékeket felvevő \(\chi^2\) eloszlásra kell támaszkodnunk. A \(X \sim {}_{\nu}\chi^2\) eloszlás momentumai
\[\begin{equation} \mathbf{E}(X)=\nu\qquad\mathbf{D}^2(X)= 2 \nu \tag{8.11} \end{equation}\]
A 8.2. ábrán a \(\chi^2\) eloszlás sűrűségfüggvénye látható különböző \(\nu\) szabadságfokok mellett.
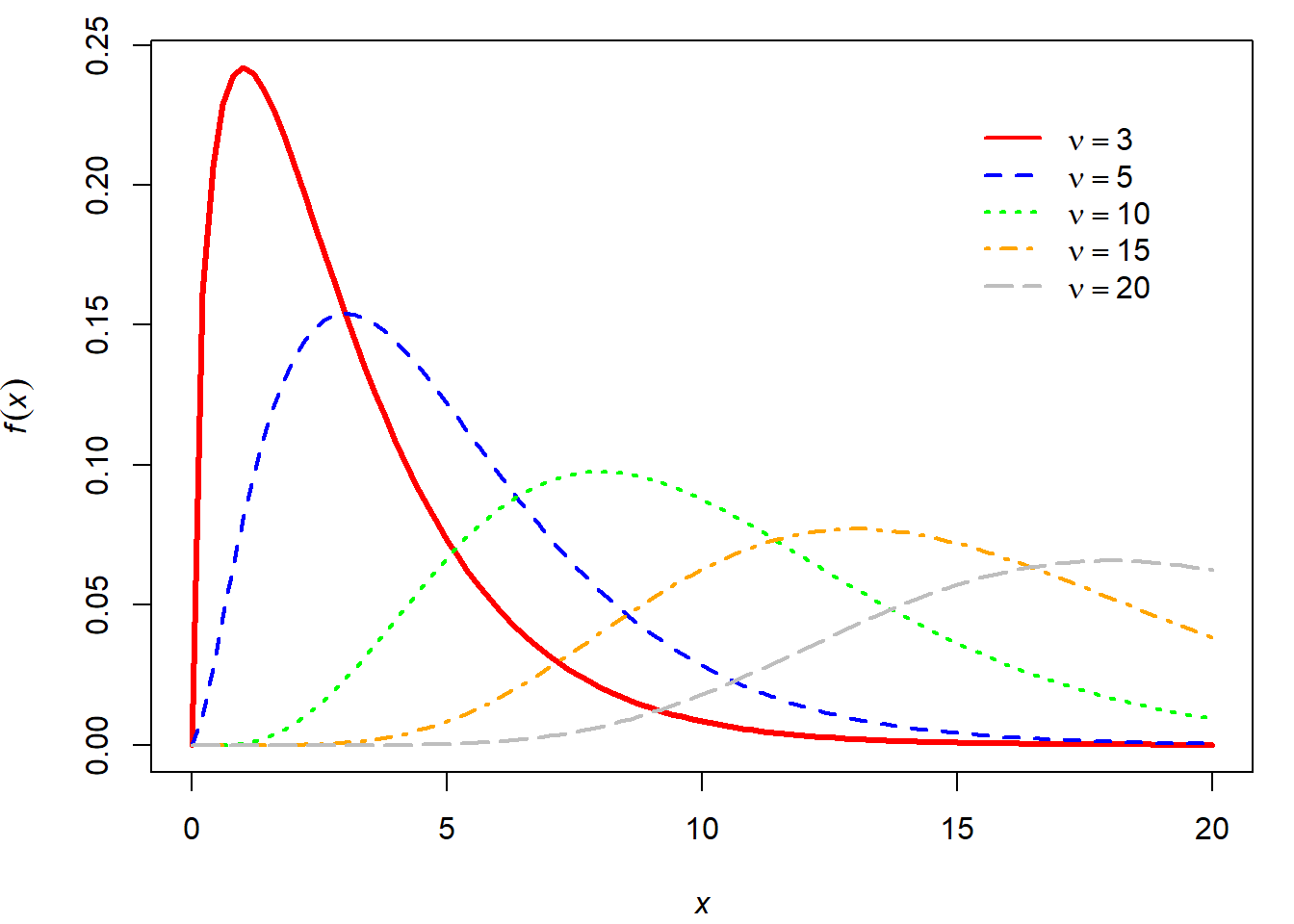
Ábra 8.2: Különböző szabadságfokú khí-négyzet eloszlások
A \(\chi^2\) eloszlás különböző szabadságfokokhoz tartozó kvantilisei erre a célra készített táblázatokból, vagy statisztikai szoftverekből is kinyerhetők. Az eloszlás nem szimmetrikus, amit a kvantilisek meghatározásakor figyelembe kell vennünk.
A \(\nu = 15\) szabadságfokú \(\chi^2\) eloszlás esetén keressük azt a két kvantilist, melyek 5-5%-ot vágnak le az eloszlás két oldaláról. Ekkor szoftver, vagy táblázat segítségével megállapítható, hogy a keresett alsó kvantilis \[ {}_{15}\chi^2_{0{,}05} = 7{,}261 \] a felső kvantilis pedig \[ {}_{15}\chi^2_{0{,}95} = 24{,}996 \]
Azaz 7,261 és 24,996 közötti található a \({}_{15}\chi^2\) eloszlás középső 90%-a. Itt kell megjegyeznünk, hogy ez az intervallum olyan értelemben középső, hogy balra és jobbra is 5-5%-ot vágunk le, ez azonban nem a legrövidebb intervallum, a gyakorlatban azonban ezt szokás alkalmazni. A legrövidebb intervallum megkeresése túlmutat tananyagunk keretein.Összefoglalva tehát a \(\sigma^2\) varianciájú sokaságból vett \(n\) elemű mintákból számított \(S^2\) valószínűségi változóról azt tudjuk, hogy várható értéke pontosan a sokasági variancia (lásd (8.9)). Ezen felül, amennyiben a sokaság normális, úgy a (8.10) valószínűségi változó \({}_{n-1}\chi^2\) eloszlást követ. Fontos újfent hangsúlyozni, hogy a variancia mintavételi eloszlása esetén csak abban az esetben tudunk következtetéseket levonni (akkor ismerjük a mintavételi eloszlást), ha a sokaság jó közelítéssel normális eloszlású. Az átlag esetén látott Centrális határeloszlás-tételre itt nem támaszkodhatunk, azaz pusztán a nagy minta alapján nem feltételezhetjük a \(\chi^2\) eloszlást. Alkalmazása előtt a normalitást a minta alapján ellenőrizni kell.
Legyen \(X\) normális eloszlású sokaság, \(\sigma = 5\) szórással. A mintavételi eloszlás megértéséhez készítettük a 8.3. ábrát, ami egyszerűen úgy készült, hogy egy \(\sigma = 5\) szórású normális eloszlásból \(n=16\) elemű mintákat vettünk 100000-szer, majd kiszámítottuk a (8.10) változó mintáról mintára ingadozó értékét. A 100000 realizáció ugyan nem az összes lehetséges minta, azonban az ezek alapján rajzolt hisztogram és az elméleti görbe láthatóan jól illeszkednek egymásra. Az ábrán jelöltük az előző példában kiszámított két kvantilis értékét (7,261 és 24,996) is.
Tudjuk tehát, (8.10) alapján, hogy \[ \mathbf{P}\left(7{,}261 < \frac{15 S^2}{25} < 24{,}996 \right) = 0{,}9 \] amiből egyszerű algebrai átalakítások után adódik, hogy \[ \mathbf{P}\left(3{,}479 < S < 6{,}454 \right) = 0{,}9 \] azaz a mintabeli szórás az esetek 90%-ában 3,479 és 6,454 közé esik, ha \(n = 16\) elemű mintát veszünk egy \(\sigma = 5\) szórású normális eloszlásból.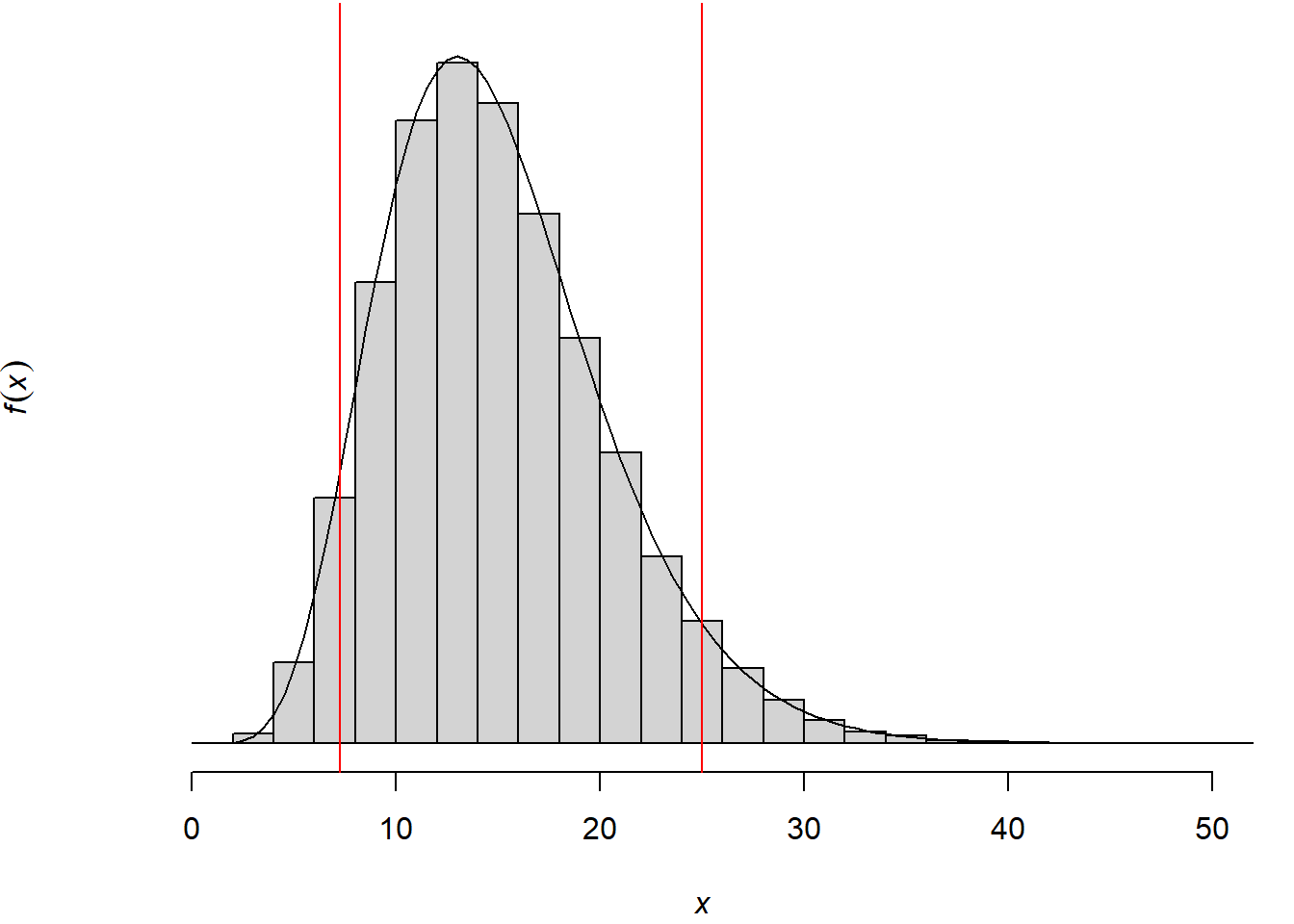
Ábra 8.3: A varianciához kapcsolódó valószínűségi változó mintavételi eloszlása
A jelölés nem keverendő össze az \(i\). sokasági értékkel, sajnos a rengeteg fogalom mellett nehéz elkerülni az azonos jelölést. Törekszünk rá, hogy mindig egyértelmű maradjon a jelölésrendszer.↩︎
Feltétel továbbá, hogy a sokaság varianciája véges, de ez a gyakorlati eseteinkben minden esetben teljesül.↩︎
A pontossághoz hozzátartozik, hogy mivel az alapsokaságok végtelen sok értéket tartalmaznak, ezért a lehetséges minták száma is végtelen. A végtelen sok minta kiválasztására nem vállalkoztunk, ábránként 100000 mintavétel történt.↩︎
A binomiális eloszlás tárgyalása során.↩︎
Ejtsd: khí-négyzet eloszlás↩︎