3.2 Osztályközös gyakorisági sor

Arra, a fejezet elején feltett kérdésünkre, hogy milyen struktúrában helyezkednek el az adataink, egy másik megközelítés, és egy másik statisztikai ábra is választ adhat. A megközelítést osztályközös gyakorisági sornak, az ábrát pedig hisztogramnak hívjuk.

Míg a 3.1. fejezetben taglalt kvantilisek esetén a két szomszédos kvantilis között található sokasági elemek száma állandó, és az információt az ő távolságuk hordozza, addig az osztályközös gyakorisági sorok esetén épp fordított a megközelítés: (alapesetben) azonos távolságra lévő pontokat jelölünk ki, majd azt vizsgáljuk, hogy hány darab sokasági megfigyelés esik az így kialakított kategóriákba, vagy más szóval osztályközökbe. Az így kialakított statisztikai sort osztályközös gyakorisági sornak nevezzük. Tananyagunkban egyenlő hosszúságú osztályközös gyakorisági sorokra koncentrálunk, de elvileg készíthetünk egymástól eltérő hosszúságú osztályközöket is.

Az osztályközös gyakorisági sor általános sémája a 3.1. táblázatban látható, \(J\) osztályköz feltételezésével. Az első osztályköz alsó és az utolsó osztályköz felső határa azért került zárójelbe, mert ezek gyakran nyitottak, azaz nincsenek megadva, például az \(X_1^{\text{felső}}\) értékkel egyenlő, vagy attól kisebb valamennyi megfigyelés az első osztályközbe tartozik.

Táblázat 3.1: Osztályközös gyakorisági sor
osztályköz	gyakoriság
\(\left(X_1^{\text{alsó}}\right)\) - \(X_1^{\text{felső}}\)	\(F_1\)
\(X_2^{\text{alsó}}\) - \(X_2^{\text{felső}}\)	\(F_2\)
\(\dots\)	\(\dots\)
\(X_J^{\text{alsó}}\) - \(\left(X_J^{\text{felső}}\right)\)	\(F_J\)
Összesen	\(N\)

Az osztályközök számának, valamint az osztályközök határainak meghatározására nincs egyetlen jó megoldás, néhány fontos szempont az alábbiakban foglalható össze:

tipikusan ajánlott egyenlő hosszúságú osztályközök alkalmazása,
áttekinthető, egyértelmű, teljes (nyitott alsó és felső közök) legyen az osztályközös gyakorisági sor, minden megfigyelés pontosan egy osztályba tartozzon, azaz tisztázni kell az osztályköz határra eső megfigyelések helyét,
lehetőleg ne legyenek üres (0 gyakoriságú) osztályközök, ami néhány extrém kiugró értéknél jelenthet gondot, erre szintén megoldás a nyitott osztályköz,
"szép" osztályköz határok (az Excel jellemzően ezt a kritériumot nem teljesíti, más szoftverek, pl. az R igen), ami alatt azt értjük, hogy lehetőség szerint kerek, vagy kevés tizedessel rendelkező, jól azonosítható törtek legyenek a határok,
több különböző szabály/képlet is van az osztályközök számára vonatkozóan, fő szabályként a minél több adat, megfigyelés egyre részletesebb (több osztályközt tartalmazó) gyakorisági sort engedélyez.

Az osztályközös gyakorisági sorhoz tartozó statisztikai ábra neve hisztogram, mely a vízszintes tengelyen az osztályközöket tartalmazza, míg a függőleges tengelyen a gyakoriságokat.

A 3.3 ábra alapján jól látható, hogy nagyon különböző sokasági eloszlások képzelhetőek el, itt is ugyanazokat a sokaságokat ábrázoltuk hisztogram segítségével, mint a boxplotok segítségével a 3.1. ábrán:

szimmetrikus, nem túl lapos, nem túl csúcsos
szimmetrikus, lapult eloszlás
szimmetrikus, csúcsos eloszlás
jobboldali aszimmetria, csúcsos eloszlás
baloldali aszimmetria, csúcsos eloszlás

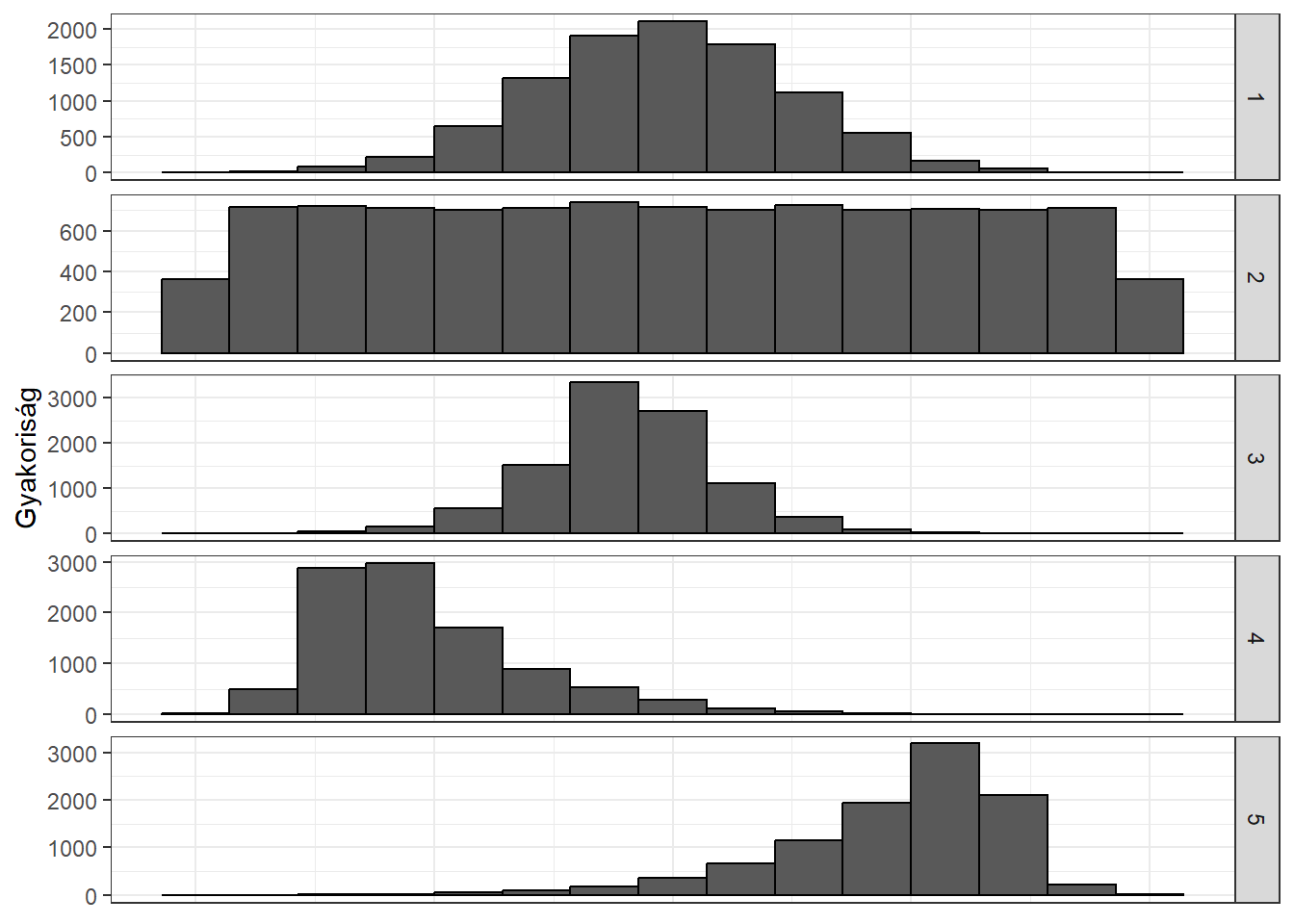
Ábra 3.3: Különböző eloszlással rendelkező sokaságok alapján készített hisztogramok

Készíthetünk gyakorisági sort a TOP100 vállalat márkaértékei alapján. Legyenek az osztályközök 40 milliárd dollár hosszúak, és az első osztályköz kezdődjön 0-tól! (Vegyük észre, hogy más értékeket is választhattunk volna, ráadásul a példánk nem is teljesíti az üres osztályközökkel kapcsolatos szempontot!) Ekkor a gyakorisági sor:

Táblázat 3.2: Osztályközös gyakorisági sor a TOP100 adatok alapján
osztályköz	gyakoriság
-40]	74
(40-80]	13
(80-120]	5
(120-160]	2
(160-200]	2
(200-240]	2
(240-280]	0
(280-	2
összesen	100

Az osztályközök kialakításakor a határokat úgy állapítottuk meg, hogy a 40 milliárdos érték még az első osztályközbe esik, a 40 milliárd feletti, 80 milliárdig bezárólag a másodikba, stb. A határra eső értékek hovatartozását érzékeltettük a ] és ( jelek alkalmazásával. A TOP100 vállalat márkaértékeire vonatkozó hisztogramok a 3.4. ábrán láthatók, két különböző osztályköz hossz esetén, azonos adatok alapján. Mindkét hisztogram alapján elmondható, hogy erős jobboldali aszimmetria figyelhető meg. Míg a baloldali ábra talán túl sok, rövid osztályköz alapján, addig a jobboldali a fenti táblázatban szereplő adatokból készült.

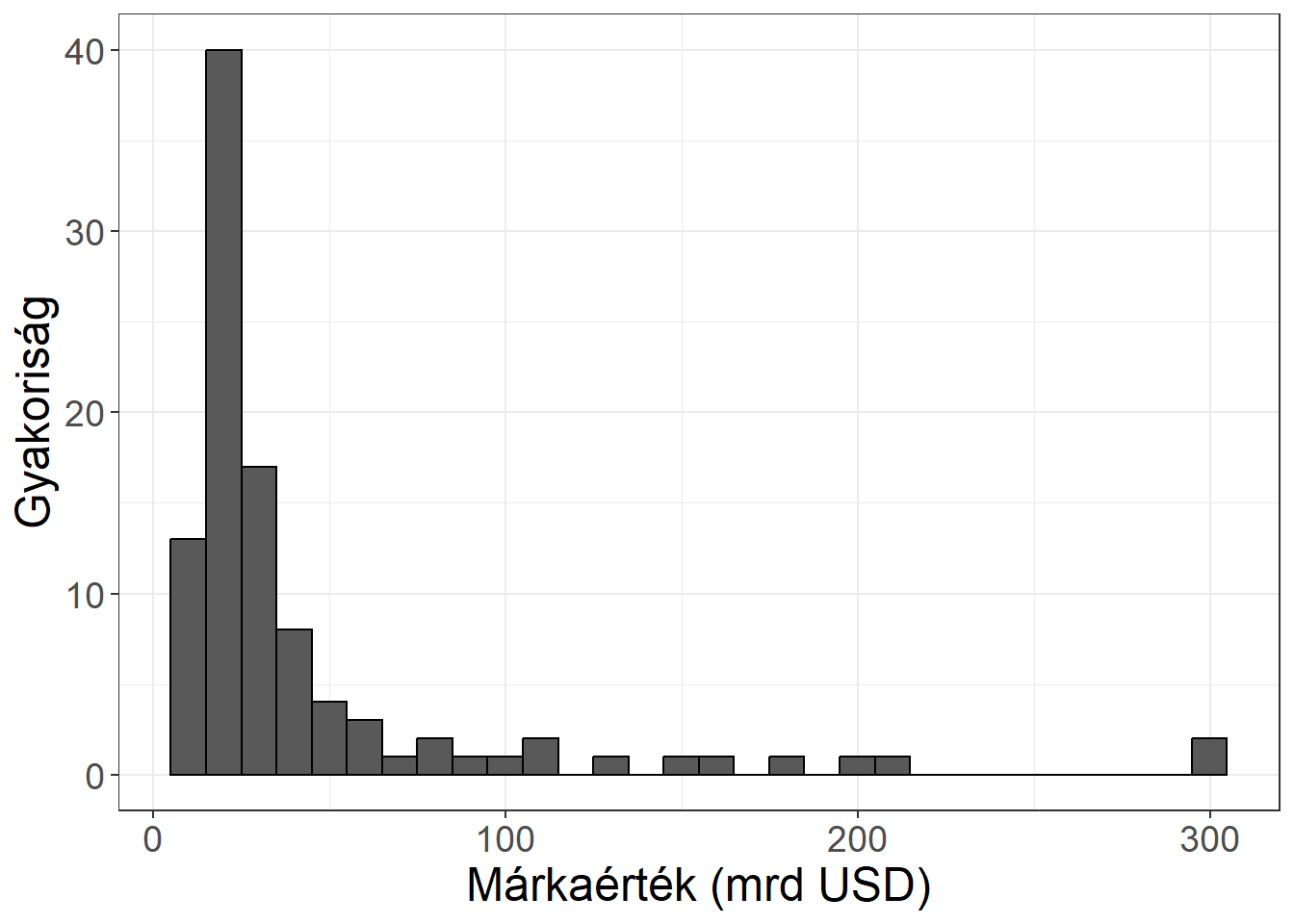
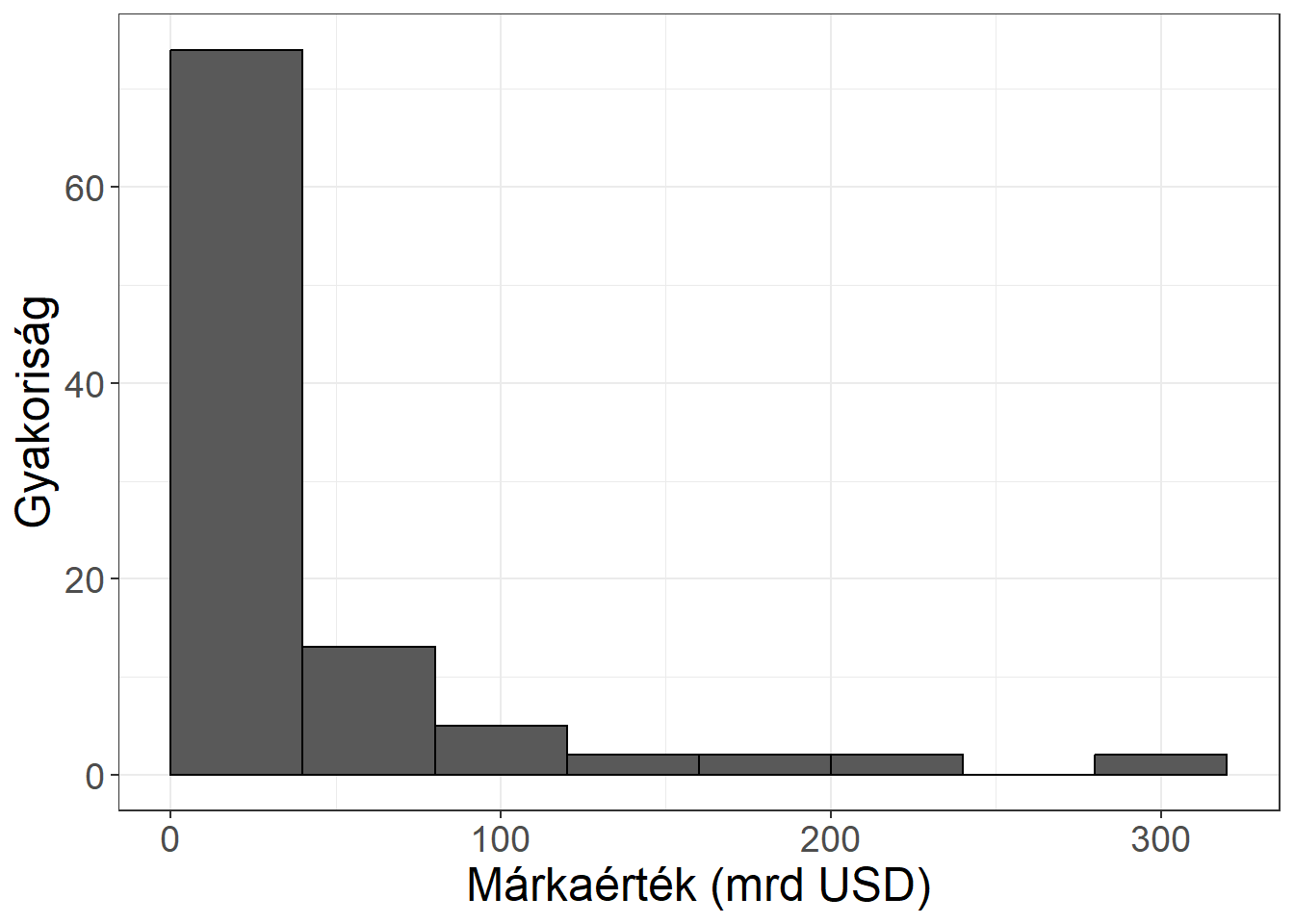
Ábra 3.4: A márkaértékek hisztogramja

A nem egyenlő hosszúságú osztályközök esete meghaladja tananyagunk kereteit, azonban a példában is látott erős aszimmetria esetén alkalmazása szükséges lehet. Ebben az esetben arra kell figyelni az ábra elkészítésekor, hogy az eltérő hosszúságú osztályközökhöz kiszámított nyers gyakoriságok torzítanak abban az értelemben, hogy az osztályköz hosszát nem veszik figyelembe, amit korrigálni kell.

Egy, a TOP100 márkaérték adatállománya alapján készített, nem egyenlő hosszúságú osztályközöket ábrázoló hisztogramokat mutat be a 3.4. ábra. Az osztályközök kezdetben 10, 25, 50, majd 100 hosszúságúak. A baloldali ábra az egyes osztályközökhöz tartozó gyakoriságokat ábrázolja, ugyanakkor nem jogos összehasonlítani egy 10 hosszúságú és egy 100 hosszúságú osztályköz gyakoriságát. A statisztikai szoftverek a szükséges korrekciót automatikusan elvégzik (jobboldali ábra).

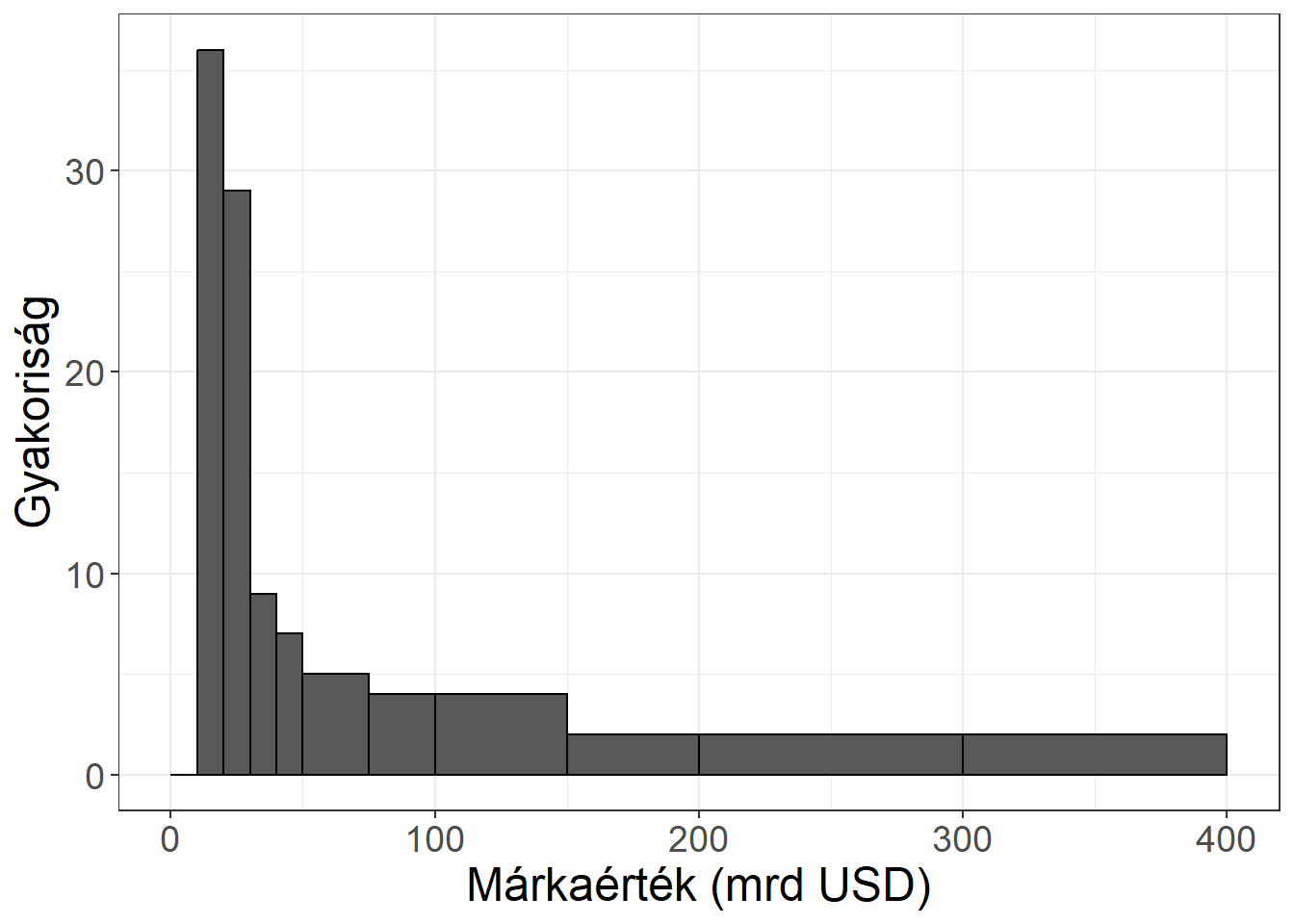
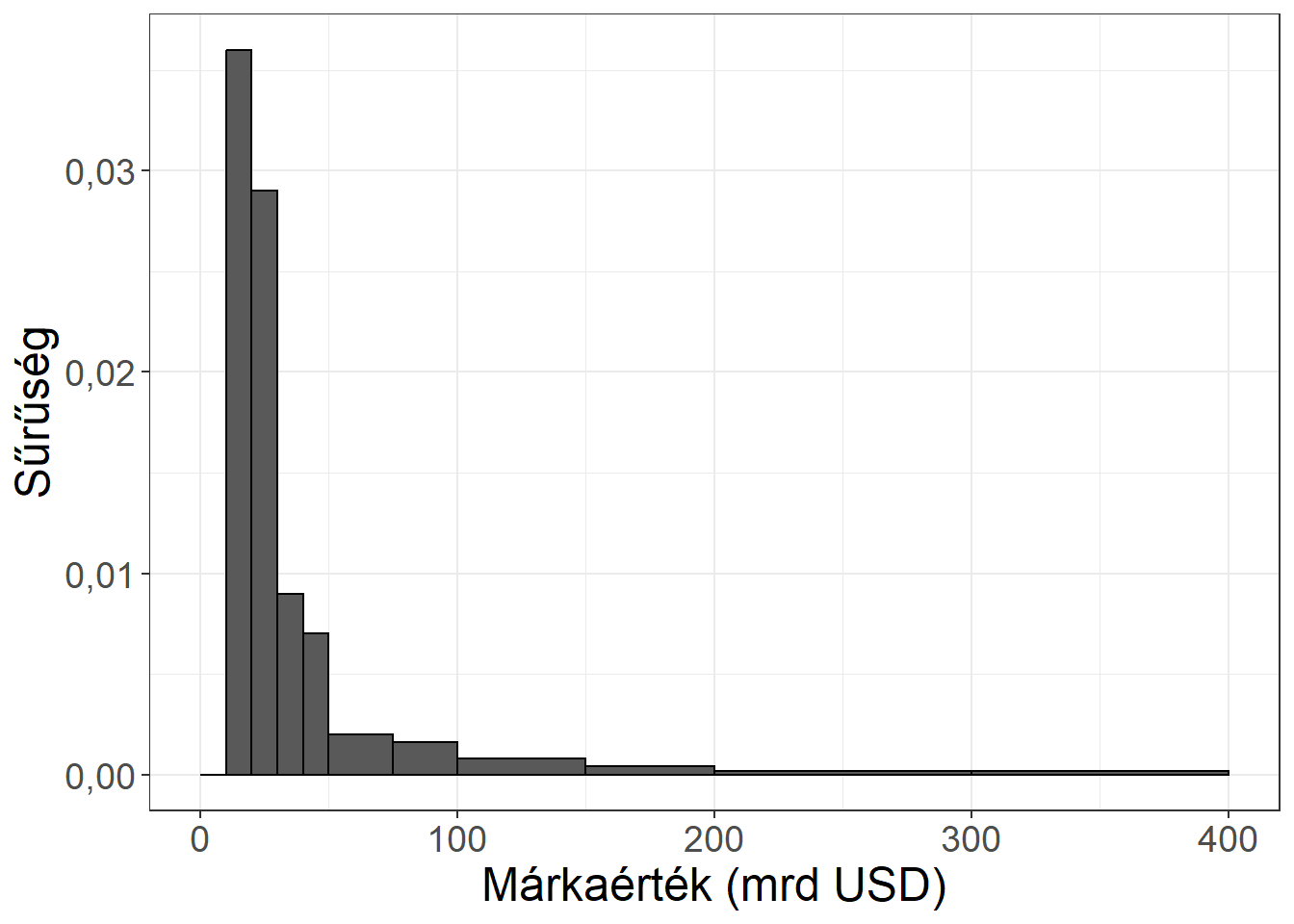
Ábra 3.5: A márkaértékek hisztogramja -- eltérő osztályköz hosszok esetén

Az osztályközös gyakorisági sor további elemzésekre is lehetőséget nyújt a hisztogram elkészítésén túl. A gyakoriságok alapján gyakran számítunk relatív gyakoriságokat (\(G_j\)), azaz megoszlási viszonyszámokat (1.5) alapján. A másik gyakran alkalmazott művelet a kumulálás, vagy felösszegzés, amit a gyakoriságokra és a relatív gyakoriságokra is elvégezhetünk.

\[\begin{equation} F_j^\prime=\sum_{k=1}^j F_k \quad G_j^\prime=\sum_{k=1}^j G_k \tag{3.2} \end{equation}\]

Azaz a \(j\). osztályköz kumulált gyakorisága az első \(j\) osztályköz gyakoriságainak az összege. A kumulált relatív gyakoriság hasonlóan képezhető. A kumulált értékek ábrázolása kumulált hisztogramot eredményez.

A gyakorisági táblázatot kiegészíthetjük a relatív gyakoriságokkal (ami 100 elemű sokaság esetén triviális), illetve kumulált értékeket is feltüntethetünk.

Táblázat 3.3: Relatív gyakoriságok és kumulált értékek a TOP100 adatok alapján
osztályköz	\(F_j\)	\(G_j\)	\(F_j^\prime\)	\(G_j^\prime\)
-40]	74	0,74	74	0,74
(40-80]	13	0,13	87	0,87
(80-120]	5	0,05	92	0,92
(120-160]	2	0,02	94	0,94
(160-200]	2	0,02	96	0,96
(200-240]	2	0,02	98	0,98
(240-280]	0	0	98	0,98
(280-	2	0,02	100	1,00
összesen	100	1	-	-

A második osztályköz kumulált gyakorisága azt jelenti, hogy 87 vállalatnak van 80 milliárd dolláros, vagy az alatti márkaértéke, ami jelen példában 87%-nak felel meg. A 3.4. ábrán látható két hisztogram párjaként, kumulált gyakoriságokból készült a 3.6. ábra két kumulált hisztogramja (a jobboldali adatai láthatók a fenti táblázatban).

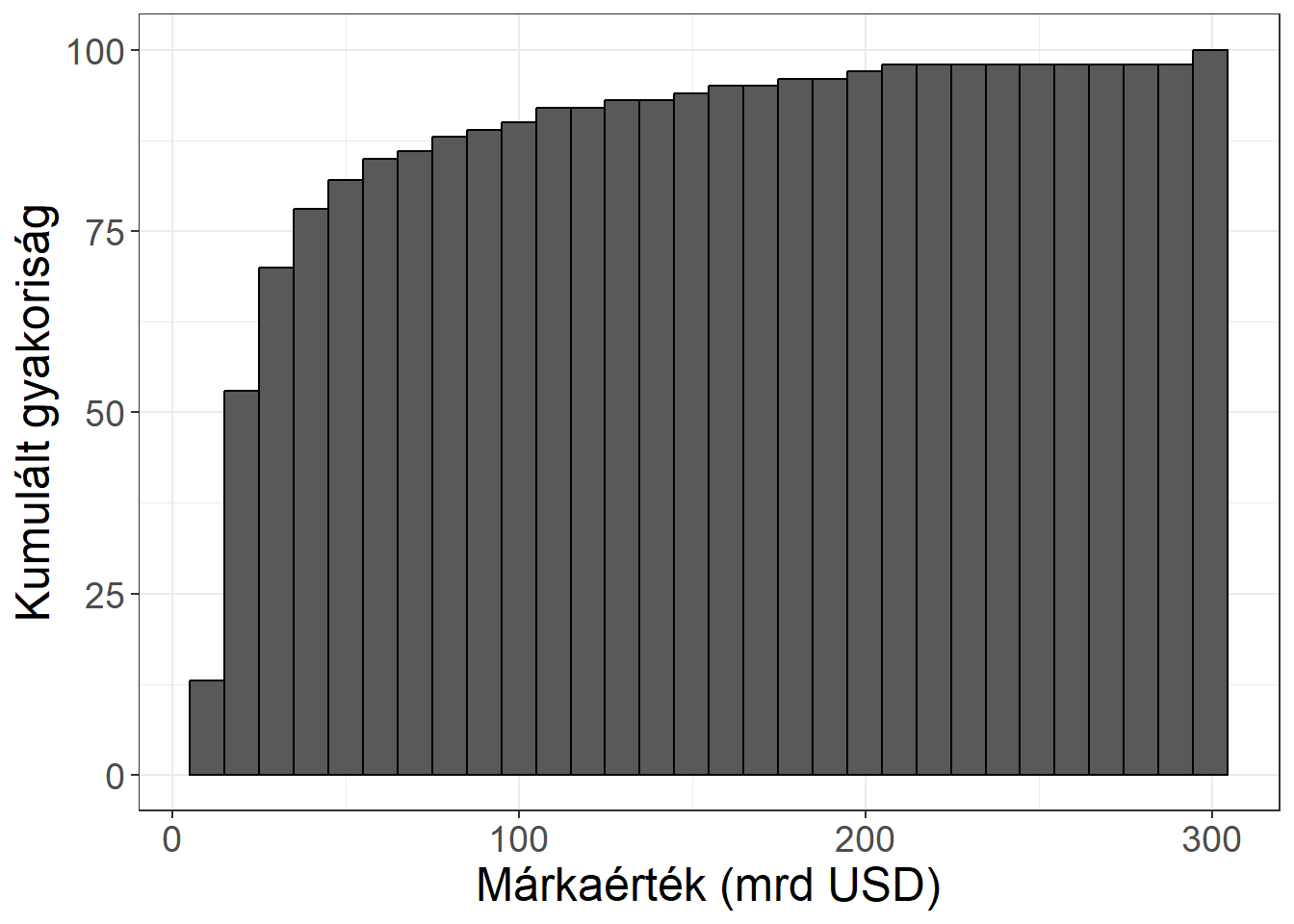
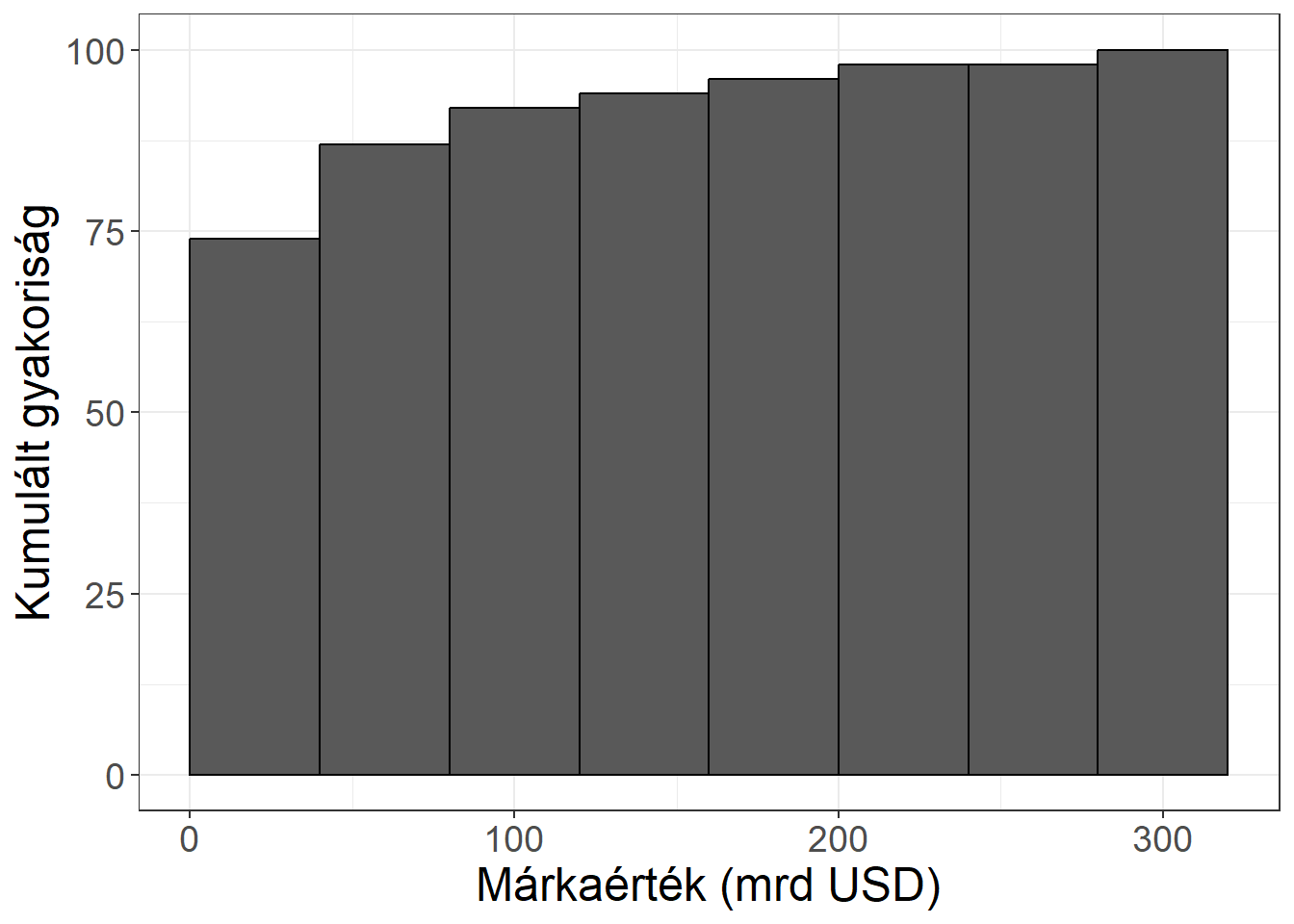
Ábra 3.6: A márkaértékek kumulált hisztogramja

A hisztogram az egyik legnépszerűbb eszköz egy sokaság elhelyezkedésének, eloszlásának bemutatására, ugyanakkor hátránya, hogy összehasonlításra kevésbé alkalmas, hiszen a két sokaságból készített hisztogramok eltakarnák egymást egy közös ábrára helyezve. Ennek orvoslására gyakran készítenek (kumulált) gyakorisági poligonokat, ami gyakorlatilag a (kumulált) hisztogram oszlopainak középpontját összekötő egyenesekből áll. A 3.7. ábra ezeket a grafikonokat mutatja be a TOP100 adatokra.

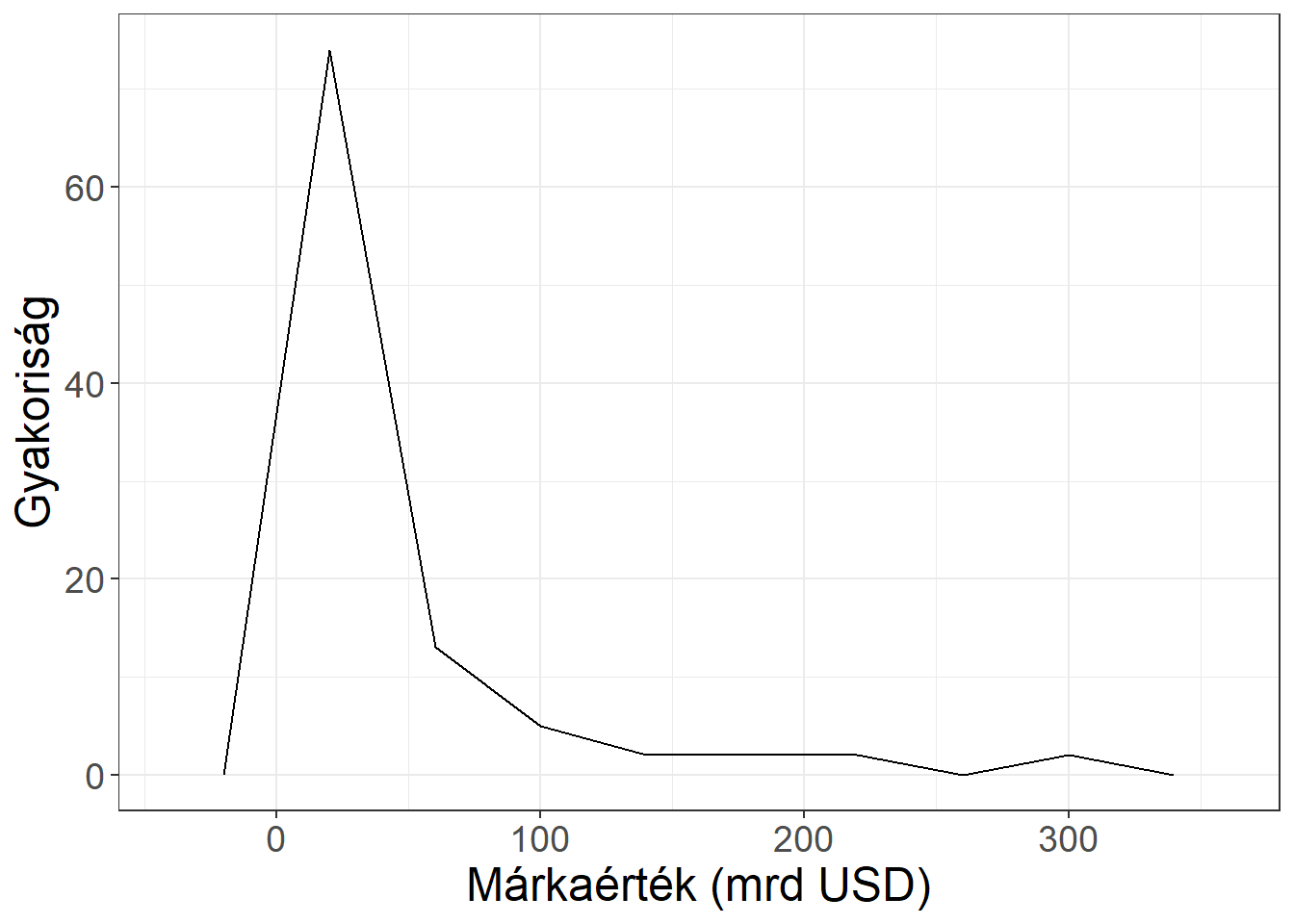
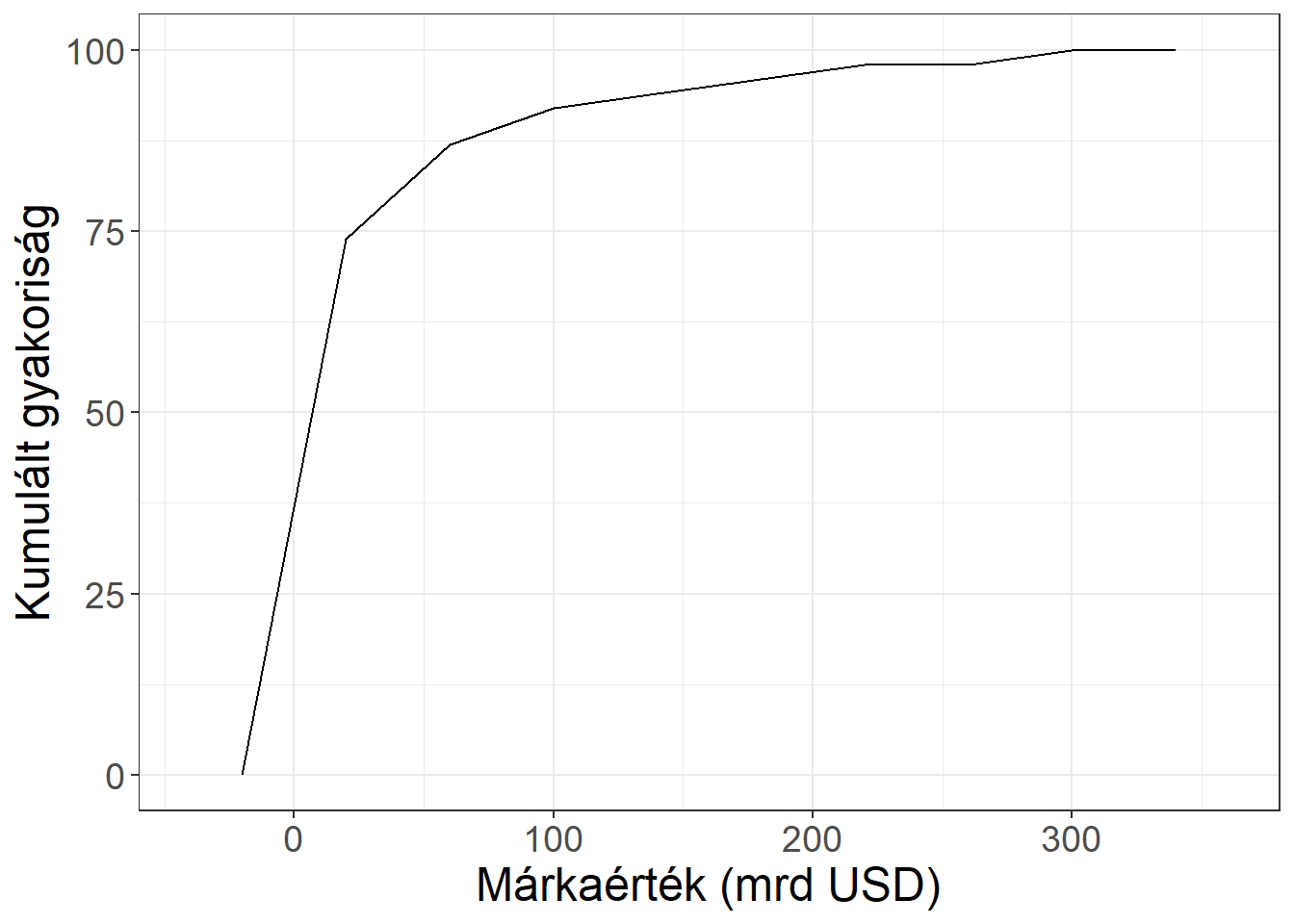
Ábra 3.7: Poligon és kumulált poligon a márkaértékre