5.3 Nevezetes diszkrét eloszlások
Sok esetben olyan jelenségeket, kísérleteket vizsgálunk, melyek egy adott sémát követnek, így a kiszámításukhoz szükséges -- egyszer már kitalált -- képleteket újra tudjuk alkalmazni kissé eltérő módon. Amennyiben például kigondoltuk, hogy az ötöslottón (ahol 90 számból 5-öt kell eltalálni) elért találatok számát milyen módon kell kiszámítani, a hatoslottó esetén már nem kell újra kigondolnunk a számítás menetét, csupán a megfelelő értékeket (későbbi szóhasználattal paramétereket) kell módosítanunk. Az ilyen, adott formula segítségével meghatározható valószínűségekkel rendelkező valószínűségi változókat nevezetes eloszlásoknak nevezzük. A nevezetes eloszlások további előnye, hogy a valószínűségek kiszámításán túl a momentumok meghatározása is jóval egyszerűbb, mint az általános (5.3), vagy (5.4) képletek segítségével.
Az alábbiakban a legegyszerűbb, leggyakrabban használt öt diszkrét nevezetes valószínűségi változót mutatjuk be, de ezen kívül is sok fontos eloszlás létezik, amelyre tananyagunk nem terjed ki. Az alábbi eloszlások logikájának megértése azonban megkönnyíti más eloszlások alkalmazását is. Azt, hogy egy \(X\) valószínűségi változó adott eloszlást követ, azt \(\sim\) módon jelöljük, amit zárójelben a már említett paraméter(ek) követ(nek).
5.3.1 Bernoulli-eloszlás
A Bernoulli-eloszlás (más néven indikátor eloszlás) a legegyszerűbb diszkrét eloszlás, mindössze két lehetséges értéke van: 0 és 1. Amennyiben egy adott, számunkra fontos, \(p\) valószínűségű esemény bekövetkezik, akkor \(X = 1\) értéket vesz fel, ellenkező esetben pedig \(X = 0\)-t. Vegyük észre, hogy egyetlen paraméter, a \(p\) értéke teljesen meghatározza az egyes lehetséges értékek valószínűségét. Az \(X\sim \text{Bern}(p)\) jelölést alkalmazva tehát a súlyfüggvény:
\[\begin{equation} \mathbf{P}(X=1)=p \text{ és } \mathbf{P}(X=0)=1-p=q \tag{5.5} \end{equation}\]
Vegyük észre, hogy a két egyszerű formula helyett a valószínűségeket a
\[\begin{equation} \mathbf{P}(X=k)=p^k \left(1-p\right)^{(1-k)}, \quad k \in \{0,1\} \tag{5.6} \end{equation}\]
módon is felírhatjuk, amely képlet már sokkal inkább hasonlít a később megismerendő eloszlásoknál látottakra. Könnyen ellenőrizhető, hogy \(k = 0\) esetre a valószínűség \(1-p\), míg a \(k=1\) esetre a valószínűség \(p\). A (5.6) formulához nagyon hasonló képlettel a későbbiekben még találkozni fogunk.
Ahogy említettük, a nevezetes eloszlások előnye, hogy a momentumok meghatározásához nem kell az általános képleteket használni, levezethetők speciális, csak az adott eloszlásra alkalmazható momentum-formulák is. Mivel ezt a Bernoulli-eloszlás esetén könnyű megtenni, ezért ezeket a levezetéseket meg is tesszük.
Meg kívánjuk tehát határozni az \(X\sim \text{Bern}(p)\) valószínűségi változó várható értékét, amihez a (5.3) általános definíciót használjuk fel, mely szerint az összes lehetséges érték és a hozzájuk tartozó valószínűségek szorzatösszege adja meg a keresett értéket:
\[\begin{equation} \mathbf{E} \left( X \right) = \sum_k x_k \cdot p_k = 0 \cdot (1-p) + 1 \cdot p = p \tag{5.7} \end{equation}\]
Hasonlóan egyszerű levezetni az \(X\sim \text{Bern}(p)\) valószínűségi változó varianciáját a (5.4) általános definíció felhasználásával:
\[\begin{equation} \mathbf{D}^2(X)=\sum_k (x_k-\mathbf{E}(X))^2 \cdot p_k = (0-p)^2 (1-p) + (1-p)^2 p = p(1-p) \tag{5.8} \end{equation}\]
Azt kaptuk tehát, hogy a \(p\) paraméter ismeretében mind a várható érték, mind a variancia könnyedén meghatározható. A Bernoulli-eloszlás klasszikus példája a pénzérme feldobás, ahol a \(p\) valószínűségű esemény lehet az, hogy fejet dobunk. Amennyiben \(p=0{,}5\), azt mondjuk, hogy a pénzérme fair.
A 5.2. ábra a Bernoulli-eloszlás súly- és eloszlásfüggvényét mutatja be.
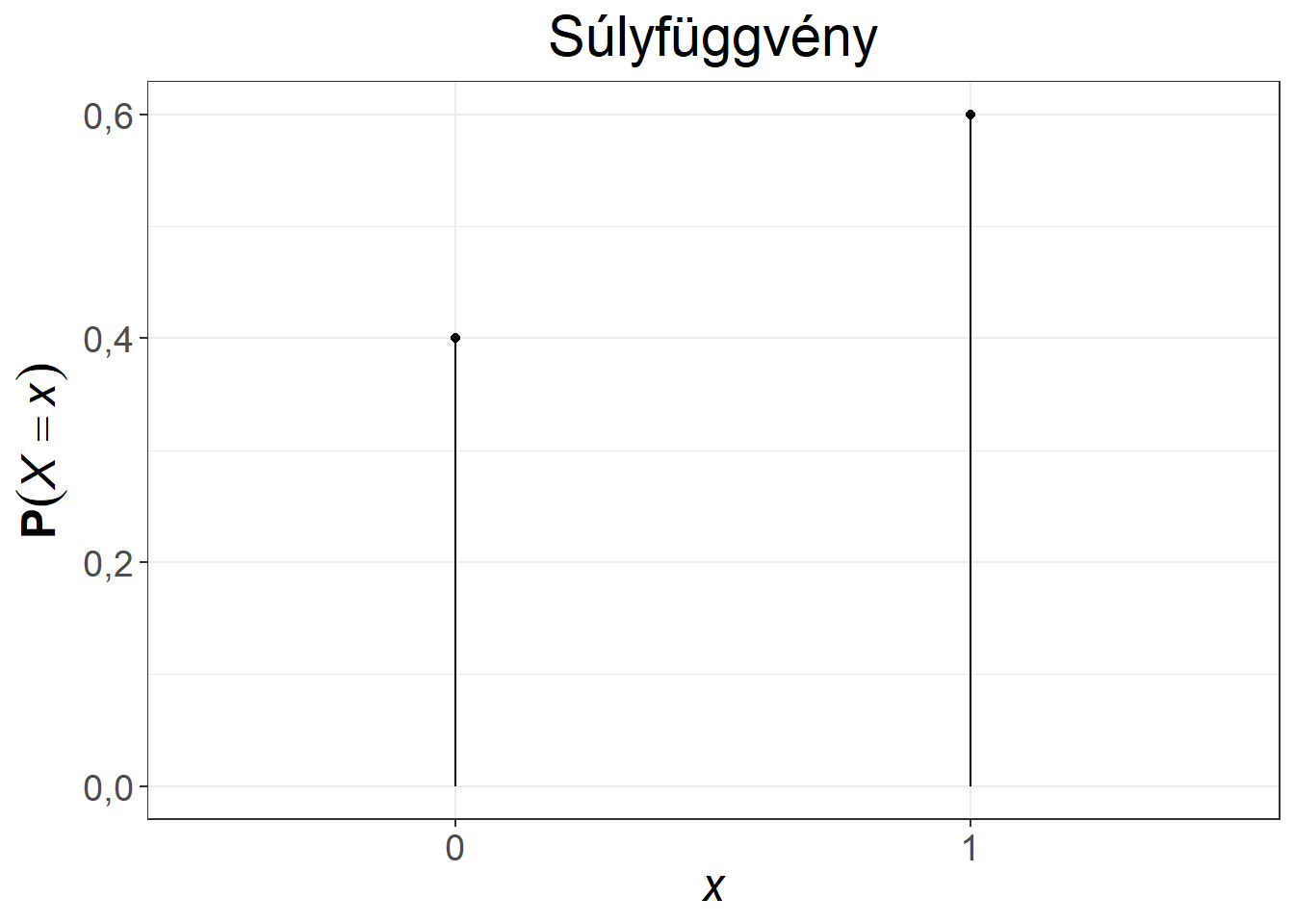
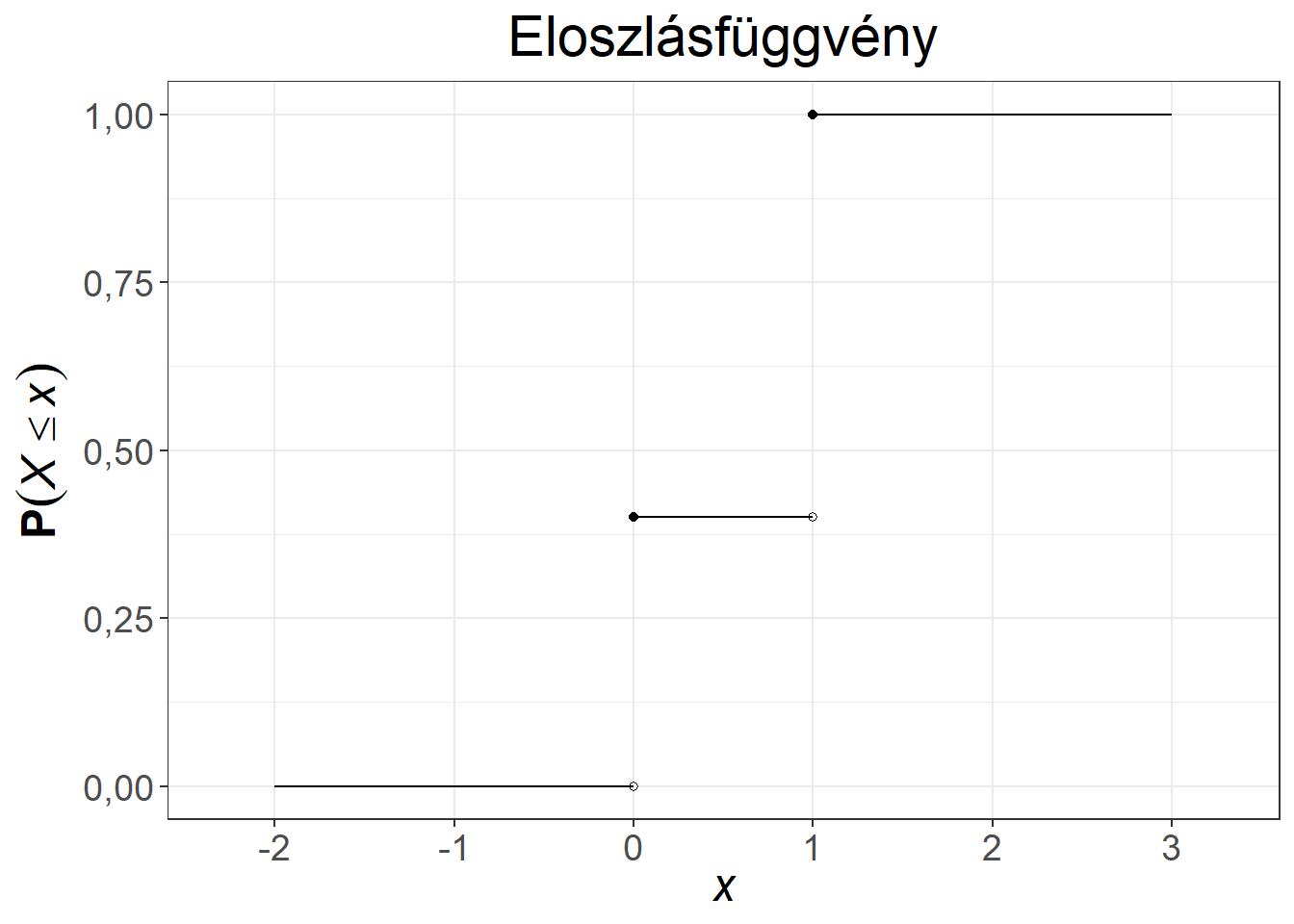
Ábra 5.2: A Bernoulli-eloszlás súly- és eloszlásfüggvénye, \(p = 0{,}6\)
5.3.2 Diszkrét egyenletes eloszlás
Amennyiben egy diszkrét valószínűségi változó \(n\) darab, egymást követő egész számmal jellemezhető lehetséges értékkel rendelkezik, melyek azonos valószínűséggel következnek be, egyenletes eloszlásról beszélünk. Az eloszlás pontos leírásához két paraméterre van szükség, amiket \(a\), a lehetséges értékek alsó határa és \(b\), a lehetséges értékek felső határa jelöl. Az \(X\sim\mathcal{U}(a,b)\) jelölést alkalmazva tehát a súlyfüggvény:
\[\begin{equation} \mathbf{P}(X=k)=\frac{1}{n} \tag{5.9} \end{equation}\]
ahol \(n=b-a+1\). A diszkrét egyenletes eloszlás momentumai a paraméterek segítségével könnyen megadhatók. A várható érték és a variancia a
\[\begin{equation} \mathbf{E}(X)=\dfrac{a+b}{2}, \qquad \mathbf{D}^2(X)=\dfrac{n^2-1}{12} \tag{5.10} \end{equation}\]
formulák segítségével számítható. A legkézenfekvőbb példa a már többször említett kockadobás, \(a = 1, b = 6\) paraméterekkel. A (5.10) képletek lehetőséget adnak a 5.2. fejezet alapján ellenőrizni a kapott várható érték és szórás eredményeket. Könnyen belátható, hogy ugyanazokat az eredményeket kapjuk (\(\mathbf{E}(X)=\dfrac{7}{2}, \mathbf{D}^2(X)=\dfrac{6^2-1}{12}=\dfrac{35}{12}\)), mint az általános képletek segítségével, de jóval egyszerűbben kaptuk meg az eredményeket, kihasználva hogy tudjuk, a kockadobás egyenletes eloszlást követ. A szóban forgó eloszlás ábráját már bemutattuk a 5.1. ábrán, így itt azt nem ismételjük meg, más paraméterű esetekre is hasonló ábrát kapnánk.
5.3.3 Binomiális eloszlás
Az egyik leggyakrabban előforduló eset és emiatt az egyik legfontosabb valószínűségi változó a mintavételhez kötődik. A binomiális eloszlás alkalmazásának feltételei az alábbiak:
- előre adott, \(n\) számú megfigyelést végzünk,
- valamennyi megfigyelés pontosan két kategóriába sorolható (sikeres, vagy sikertelen)
- minden egyes megfigyelés esetén a siker valószínűsége állandó, amit \(\pi\) jelöl,
- a megfigyelések egymástól függetlenek (pl. az első mintaelem kiválasztásának eredménye nem befolyásolja a második és azt követő mintaelemek eloszlását, vagy más szavakkal, nem változtatja meg a sokaság összetételét),
- a vizsgálatunk tárgya az összes sikeres megfigyelés száma a mintában (\(k\)).
Ezek a feltételek két gyakran előforduló gyakorlati mintavételi esetben is érvényesek:
- végtelen sokaságból vett, illetve
- véges sokaságból visszatevéssel vett
minta esetén. Általánosságban a fenti két eset az alábbiakkal írható le.
- Végtelen alapsokaságból egymástól függetlenül vett \(n\) elemű mintába az elemenként \(\pi\) valószínűségű adott tulajdonságú objektumból \(k\) darab kerül be.
- Véges, \(N\) elemű alapsokaságban \(K\) darab adott tulajdonsággal rendelkező elem van. Ebből a sokaságból visszatevéssel vett \(n\) elemű mintába \(k\) darab adott tulajdonságú elem kerül be. Ekkor a \(\pi = \frac{K}{N}\) jelöléssel élünk.
Jelölje a \(X\) valószínűségi változó a mintába kerülő, adott tulajdonsággal rendelkező objektumok számát (vagy röviden a sikerek számát). Mindkét fenti esetben azt mondjuk, hogy \(X\sim\text{Bin}(n,\pi)\), azaz \(X\) binomiális eloszlást követ, \(n\) és \(\pi\) paraméterekkel. A súlyfüggvényt az alábbi
\[\begin{equation} \mathbf{P}(X=k)=\binom{n}{k}\pi^k (1-\pi)^{n-k} \tag{5.11} \end{equation}\]
formula írja le. A képlet emlékeztet a (5.6) egyenletben látott kifejezésre. A kapcsolat a két eloszlás között igen szoros, hiszen míg a Bernoulli-eloszlás egy kísérletet írt le, addig a binomiális eloszlás \(n\) egymás követő kísérletet. Formálisan is könnyű belátni, hogy \(n\) darab \(p\) paraméterű Bernoulli-eloszlású véletlen változó összege \(n, p\) paraméterpárral rendelkező binomiális eloszlást ad. Vagy a másik oldalról, a Bernoulli-eloszlás a binomiális eloszlás speciális esete, arra az esetre, amikor \(n = 1\).
A binomiális eloszlás paramétereinek ismeretében a megismert momentumok könnyedén számíthatók:
\[\begin{equation} \mathbf{E}(X)=n\pi,\qquad\mathbf{D}^2(X)=n\pi(1-\pi) \tag{5.12} \end{equation}\]
A binomiális eloszlás súly- és eloszlásfüggvénye változatos alakot ölt a paraméterek függvényében. Az 5.3. ábra két paraméterpár esetén mutatja be a függvényeket. Az első esetben a \(\pi = 0{,}5\) választás miatt a sűrűségfüggvény szimmetrikus, illetve az eloszlásfüggvény is középpontosan szimmetrikus, míg a 0,5 feletti paraméter baloldali (hiszen a magas \(k\) értékekhez fog magas valószínűség tartozni), a 0,5 alatti paraméter jobboldali aszimmetriát (hiszen az alacsony \(k\) értékekhez fog magas valószínűség tartozni) okoz a súlyfüggvényben.
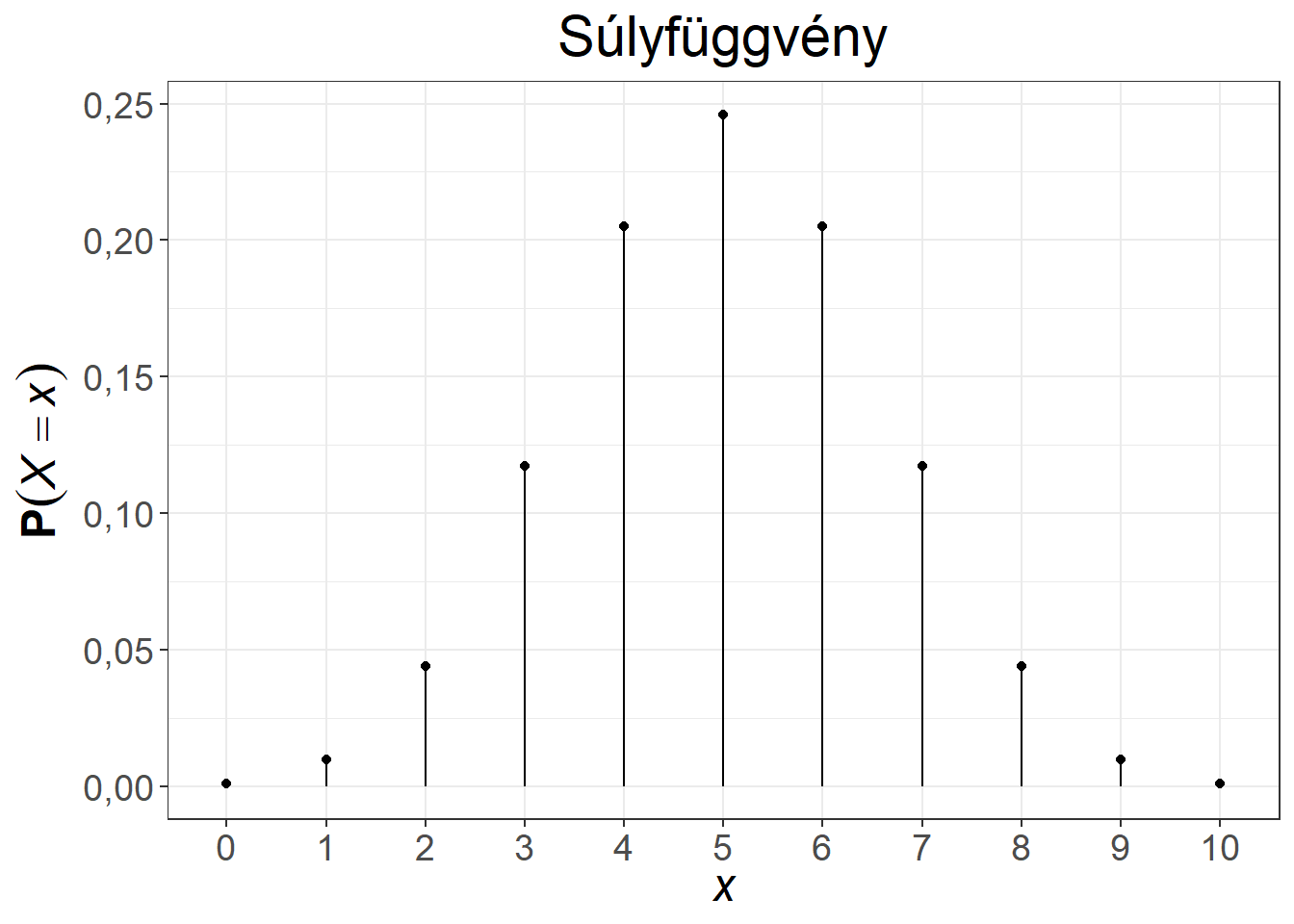
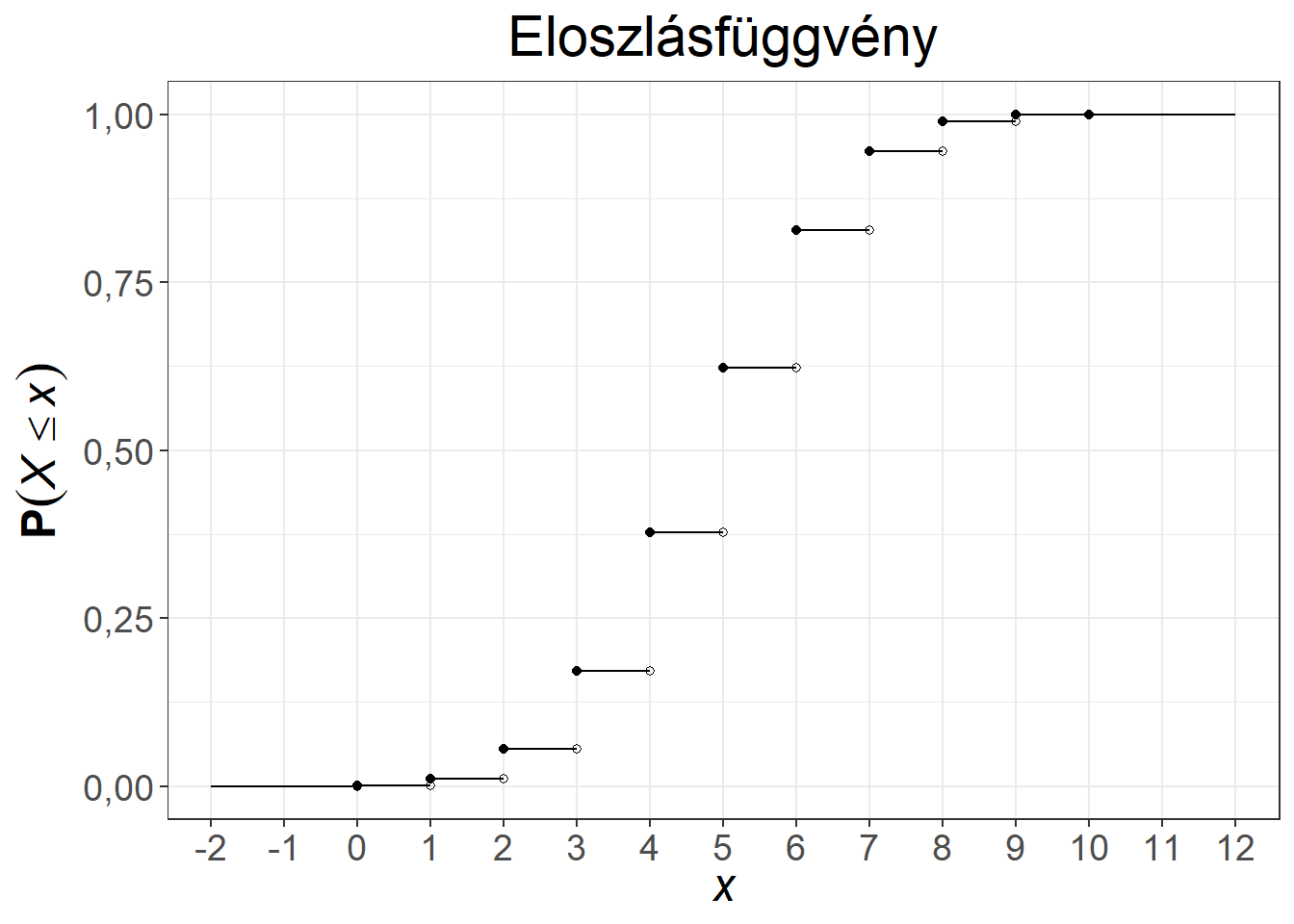
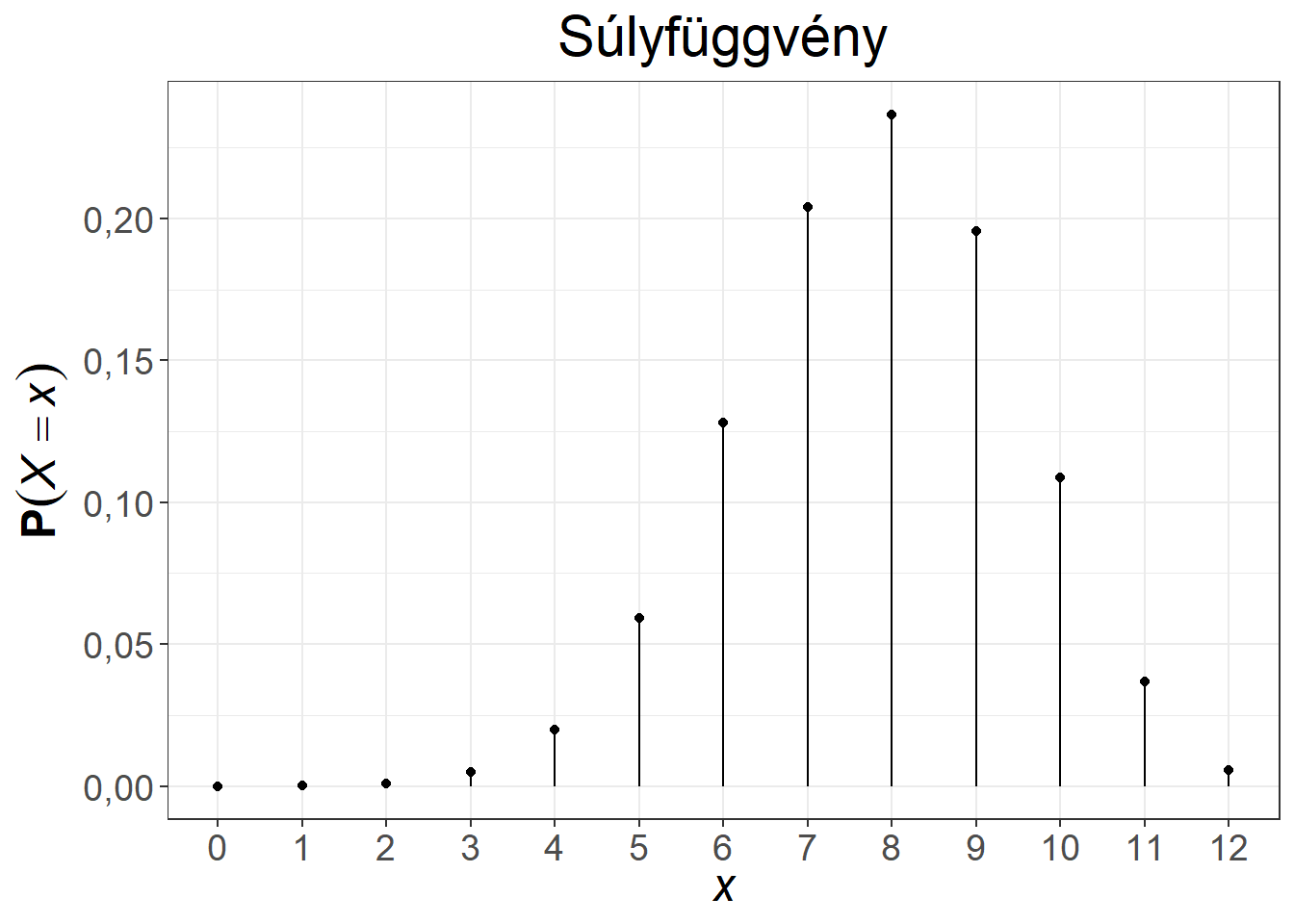
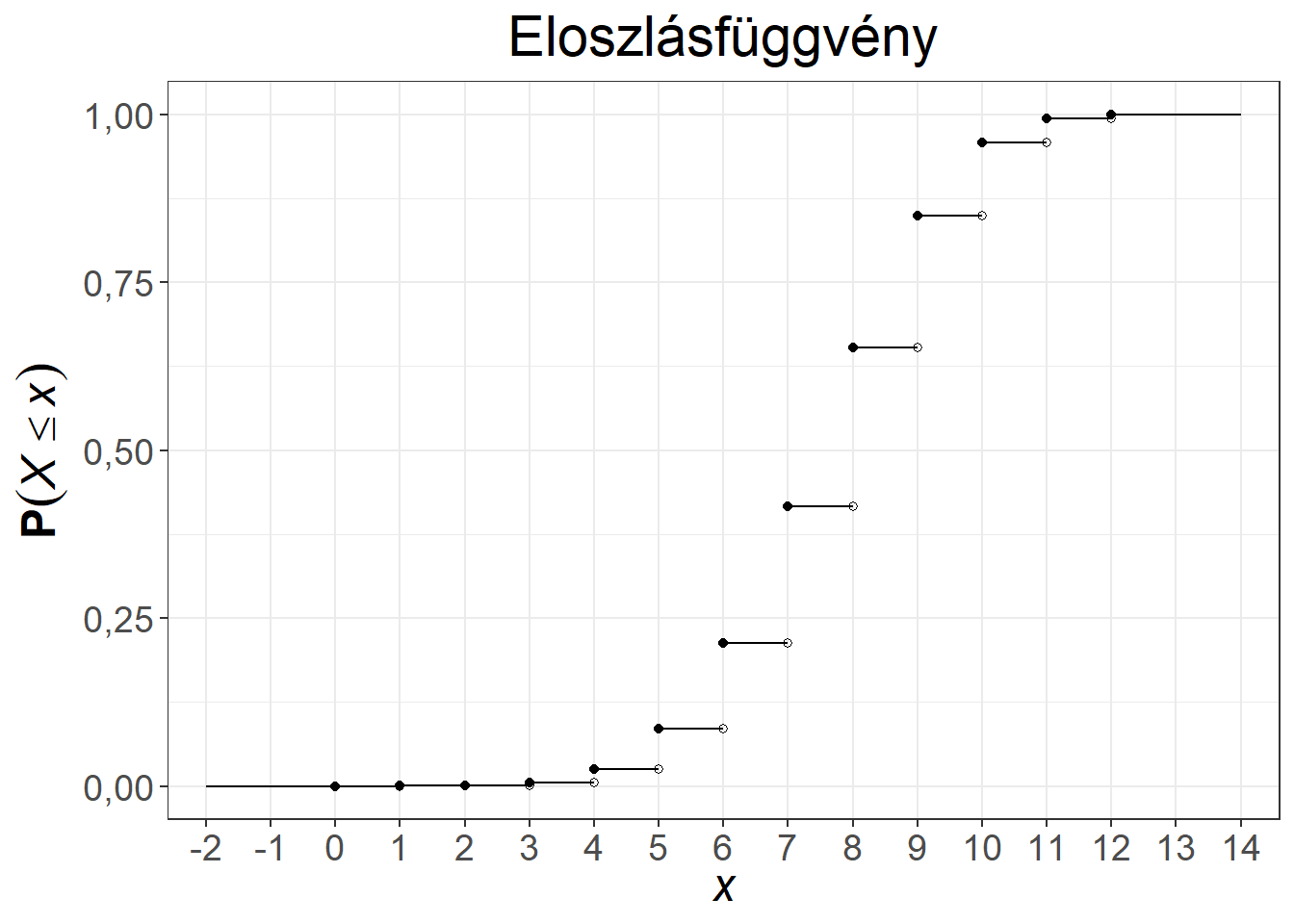
Ábra 5.3: A binomiális eloszlás súly- és eloszlásfüggvénye, \(n = 10, \pi = 0{,}5\), illetve \(n = 12, \pi = 0{,}65\)
A binomiális eloszlásra a klasszikus példa a pénzérme feldobása \(n\) alkalommal, \(X\) pedig jelölje a dobott fejek számát (azaz a fejeket tekintjük sikeres eseménynek). Ennek a modellezésére fair érme esetén az \(n, \pi=0{,}5\) paraméterpárral rendelkező binomiális eloszlás felel meg.
Itt jegyezzük meg, hogy a gyakorlatban a nagyon nagy alapsokaságot is végtelenként kezeljük. Gyakorlati szempontból egy Magyarország népességéből vett viszonylag kis elemszámú visszatevés nélküli minta is függetlennek tekinthető, gyakorlati szempontból nem változik meg a sokaság összetétele jelentősen attól, hogy az első elemeket már kihúztuk, és nem tettük őket vissza. Abban az esetben viszont, ha a minta a sokaság méretéhez képest nem elhanyagolható méretű, és a kiválasztás visszatevés nélkül történik, a binomiális eloszlás nem alkalmazható.
5.3.4 Hipergeometriai eloszlás
Az előző pontban bemutatott binomiális eloszlás a mintában előforduló sikeres esetek számához rendel valószínűségeket több különböző esetre vonatkozóan is, de a véges alapsokaságból visszatevés nélkül vett minták esetén más eloszlással kell megismerkednünk. Amennyiben annak a valószínűségére vagyunk kíváncsiak, hogy \(N\) elemű véges alapsokaságból visszatevés nélkül vett \(n\) elemű mintába, az összesen \(K\) tulajdonságú objektumból pontosan \(k\) db kerül be, akkor a hipergeometriai, vagy hipergeometrikus eloszlásról beszélünk. A \(X\sim\text{Hip}(n,K,N)\) eloszlás súlyfüggvénye a
\[\begin{equation} \mathbf{P}(X=k)=\frac{\binom{N-K}{n-k}{\binom{K}{k}}}{\binom{N}{n}} \tag{5.13} \end{equation}\]
formulával írható le. A számítás logikája tulajdonképp egyszerű, az összes lehetséges \(\binom{N}{n}\) mintából azoknak a számát szeretnénk meghatározni, amiben pontosan \(k\) adott tulajdonságú szerepel. Ennek meghatározására egyrészt a mintánkba pontosan \(\binom{K}{k}\) módon választhatunk az adott tulajdonsággal rendelkezők közül, majd -- hogy teljes legyen a minta -- ki kell választanunk az adott tulajdonsággal nem rendelkező mintaelemeket, amit \(\binom{N-K}{n-k}\) módon tehetünk meg. Mivel minden sikeres csoporthoz minden nem sikeres csoportot választhatjuk, ezért a lehetőségek számát a számlálóban összeszorozzuk.
A \(X\sim\text{Hip}(n,K,N)\) eloszlás momentumai a paraméterek ismeretében könnyen számíthatóak.
\[\begin{equation} \mathbf{E}(X)=n\frac{K}{N},\qquad\mathbf{D}^2(X)=n\frac{K}{N}\frac{N-K}{N}\frac{N-n}{N-1} \tag{5.14} \end{equation}\]
Amennyiben ezt a formulát összehasonlítjuk a binomiális eloszlás várható értékével és varianciájával a (5.12) egyenletben, és a hipergeometriai eloszlásnál is bevezetjük a \(\pi = \frac{K}{N}\) jelölést, akkor azt látjuk, hogy a két várható érték megegyezik, a varianciák pedig abban különböznek, hogy a hipergeometriai eloszlás esetén szerepel egy \(\frac{N-n}{N-1}\) tényező. Mivel ezt a különbséget a véges sokaság miatt figyelhetjük meg, a tényező neve véges szorzó. A későbbi fejezetekben még találkozni fogunk a kifejezéssel.
A hipergeometriai eloszlás klasszikus példája a lottón elért találatok valószínűsége, ami olyan szempontból speciális példa, hogy a sokaságban a kedvező esetek száma is \(K = 5\) (hiszen öt nyerőszám van) és a mintaelemszám is \(n = 5\) (hiszen öt számra kell tippelni). Ez a hipergeometriai eloszlás egyéb felhasználásai esetén nem feltétlenül van így.
A hipergeometriai eloszlás súlyfüggvénye és eloszlásfüggvénye két paraméterezés mellett az 5.4. ábrán látható.
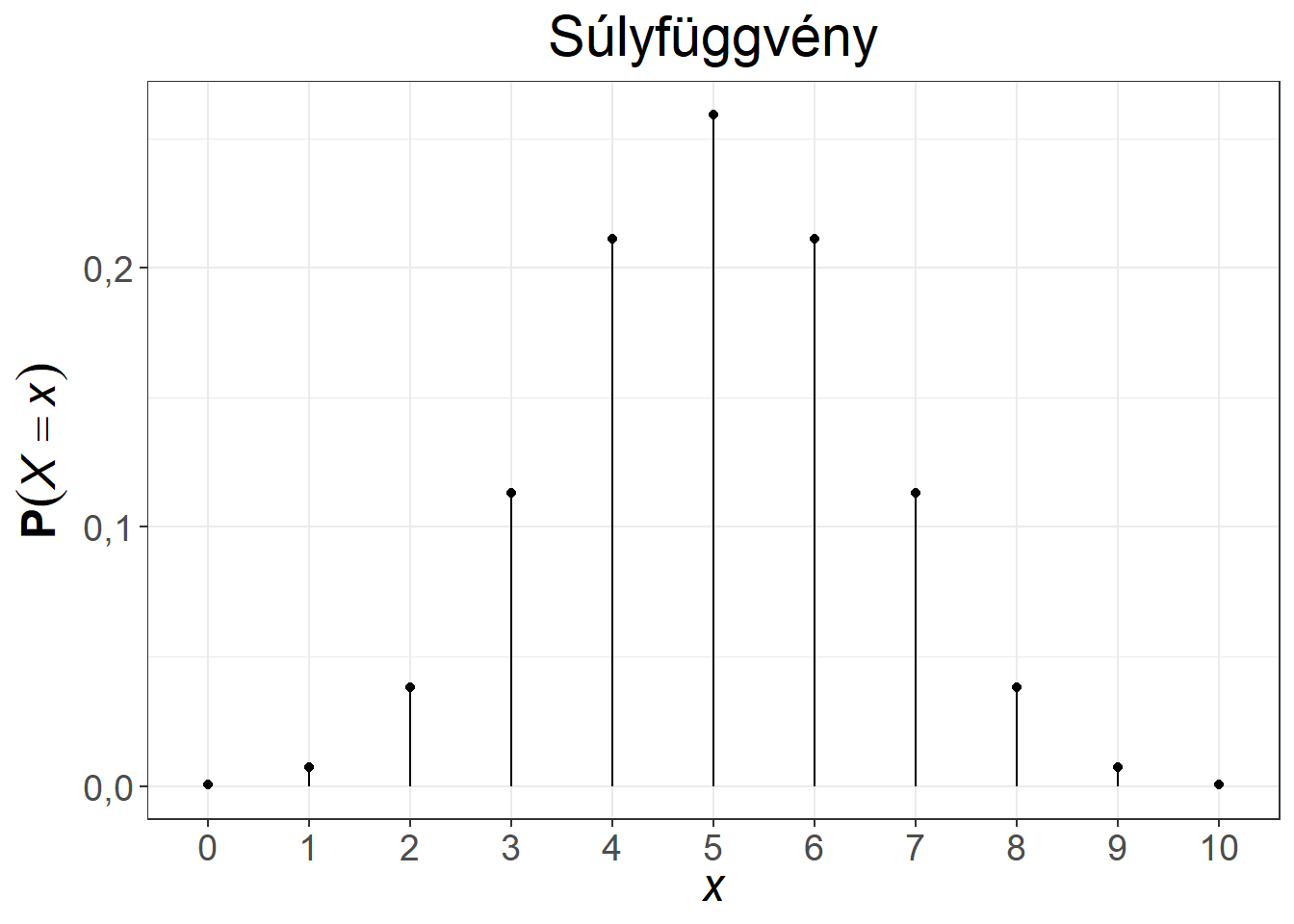
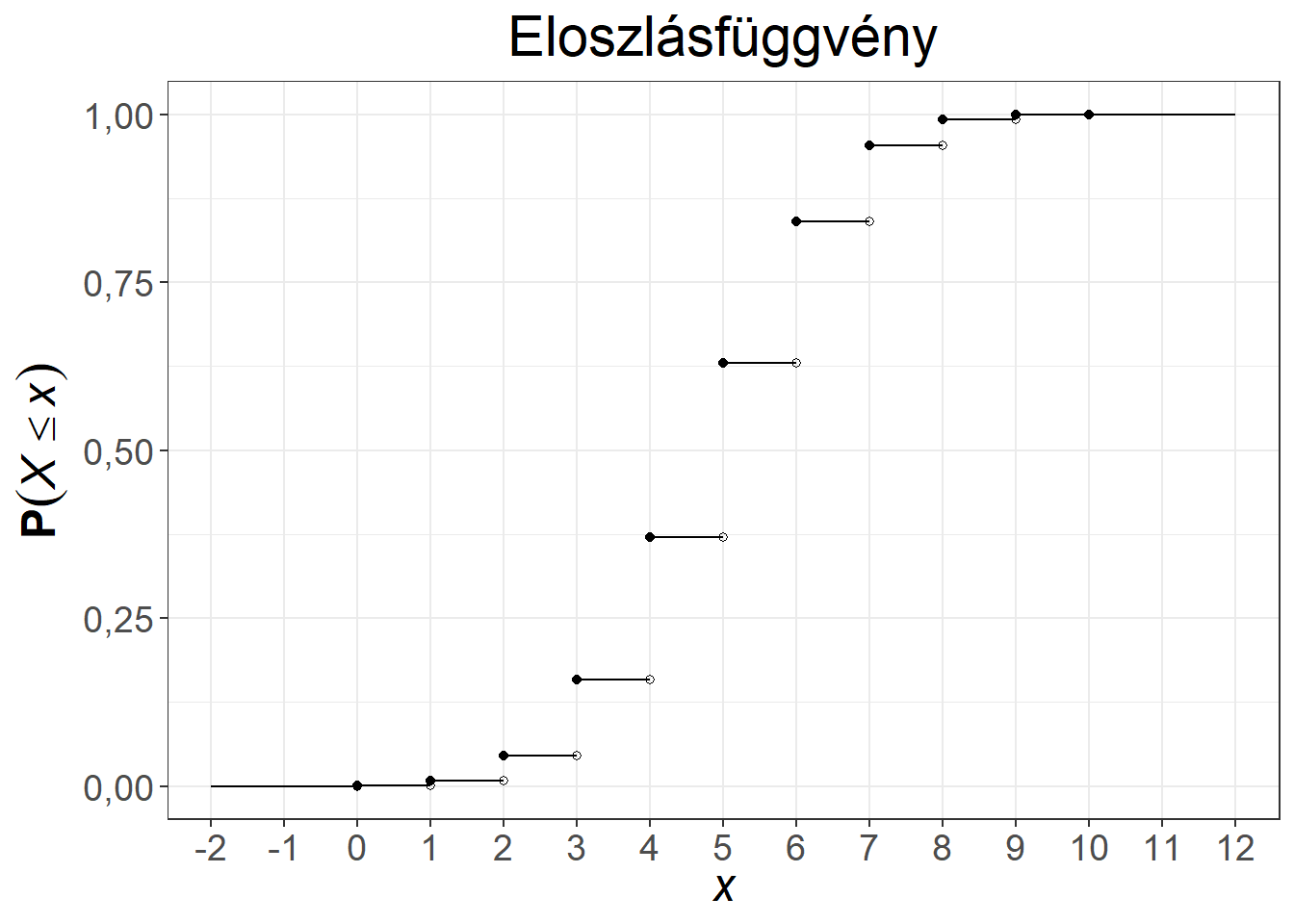
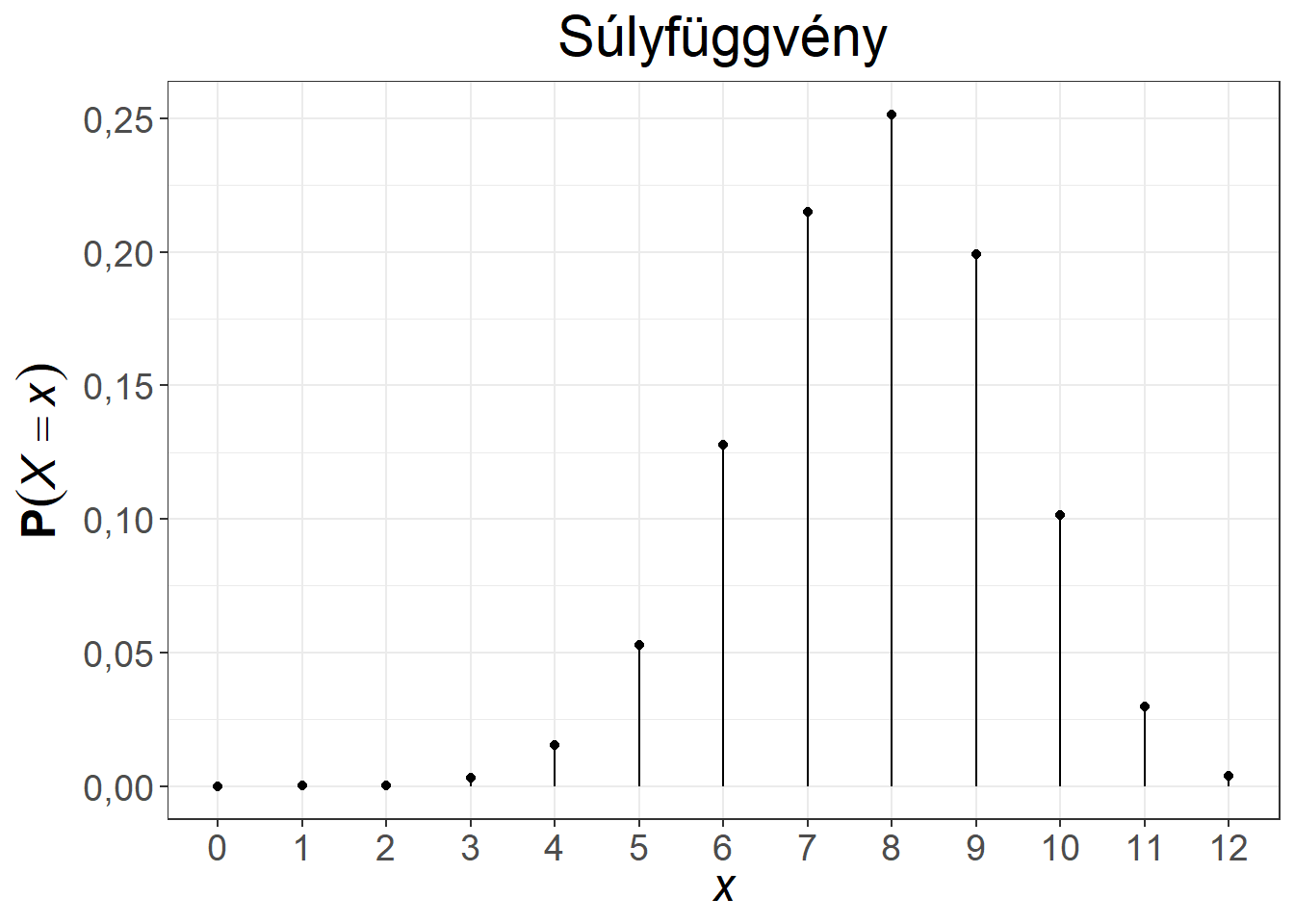
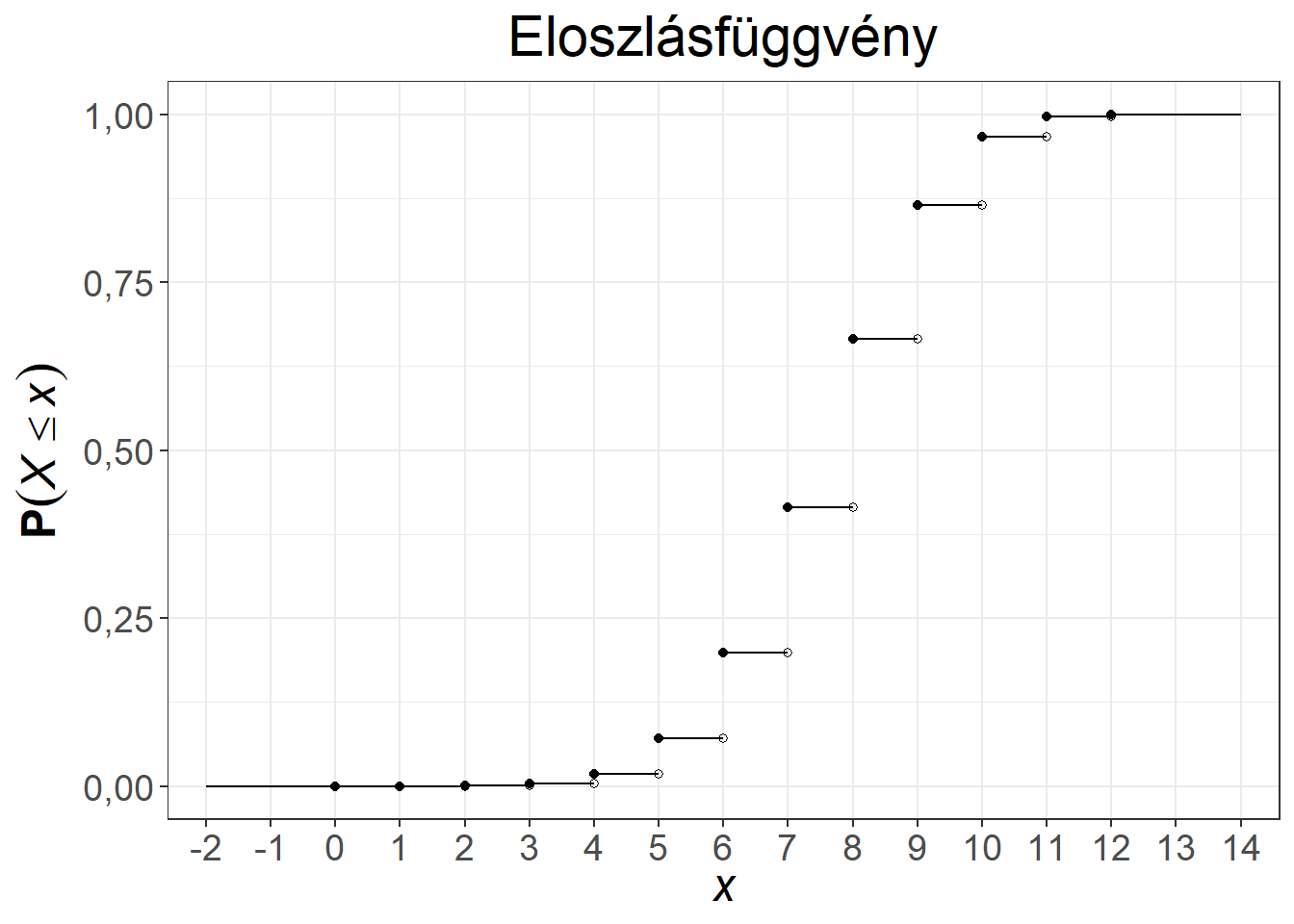
Ábra 5.4: A hipergeometriai eloszlás súly- és eloszlásfüggvénye, \(n = 10, K = 50, N = 100\), illetve \(n = 12, K = 65, N = 100\)
5.3.5 Poisson-eloszlás
A Poisson-eloszlás nem közvetlenül a mintavételhez kapcsolódik, mégis hasznos, gyakran alkalmazott eloszlás. Az eloszlás egy rögzített időtartam alatt, vagy felszínen megfigyelhető események számának valószínűségét írja le, ha az események egymástól függetlenül következnek be, állandó ráta mellett. A korábban megismert diszkrét eloszlásokkal szemben \(X\) lehetséges értékeinek nincs felső határa, azonban a legnagyobb valószínűség után az egyes kimenetelekhez tartozó valószínűség folyamatosan csökken a végtelenig. A Poisson eloszlás egyetlen paraméterrel írható le, a \(X\sim\text{Poi}(\lambda)\) eloszlás súlyfüggvényét a
\[\begin{equation} \mathbf{P}(X=k)=\frac{\lambda^k\mathrm{e}^{-\lambda}}{k!} \tag{5.15} \end{equation}\]
formula adja. A Poisson-eloszlás különleges abból a szempontból, hogy a várható értéke és varianciája megegyezik.
\[\begin{equation} \mathbf{E}(X)=\lambda,\qquad\mathbf{D}^2(X)=\lambda \tag{5.16} \end{equation}\]
A klasszikus példa a Poisson-eloszlásra az óránként egy call-centerbe érkező hívások száma. Az első közismert alkalmazása a porosz hadseregben évente halálra rúgott katonák számának modellezése volt. Az 5.5. ábra két Poisson-eloszlás első néhány értékét mutatja be.
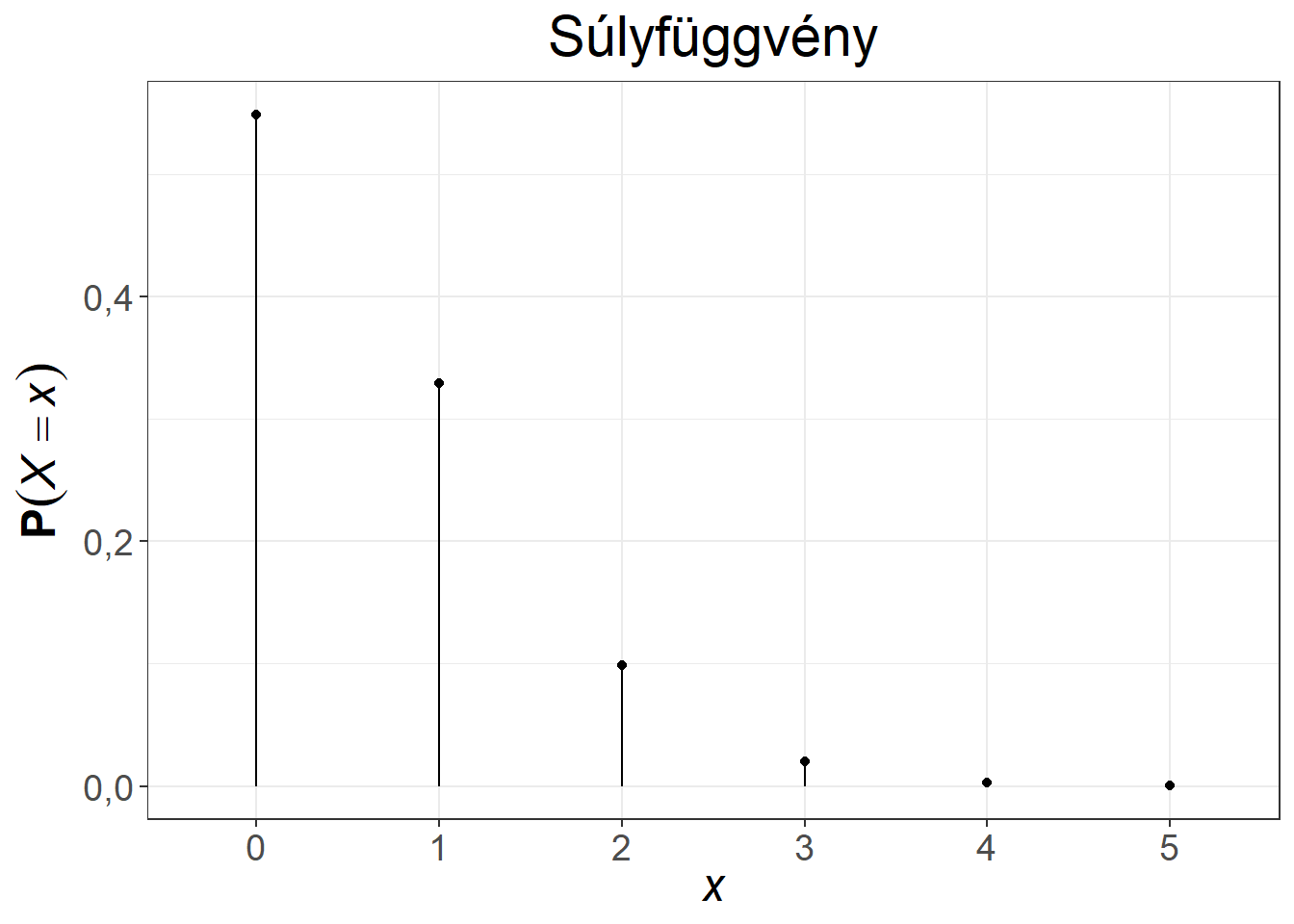
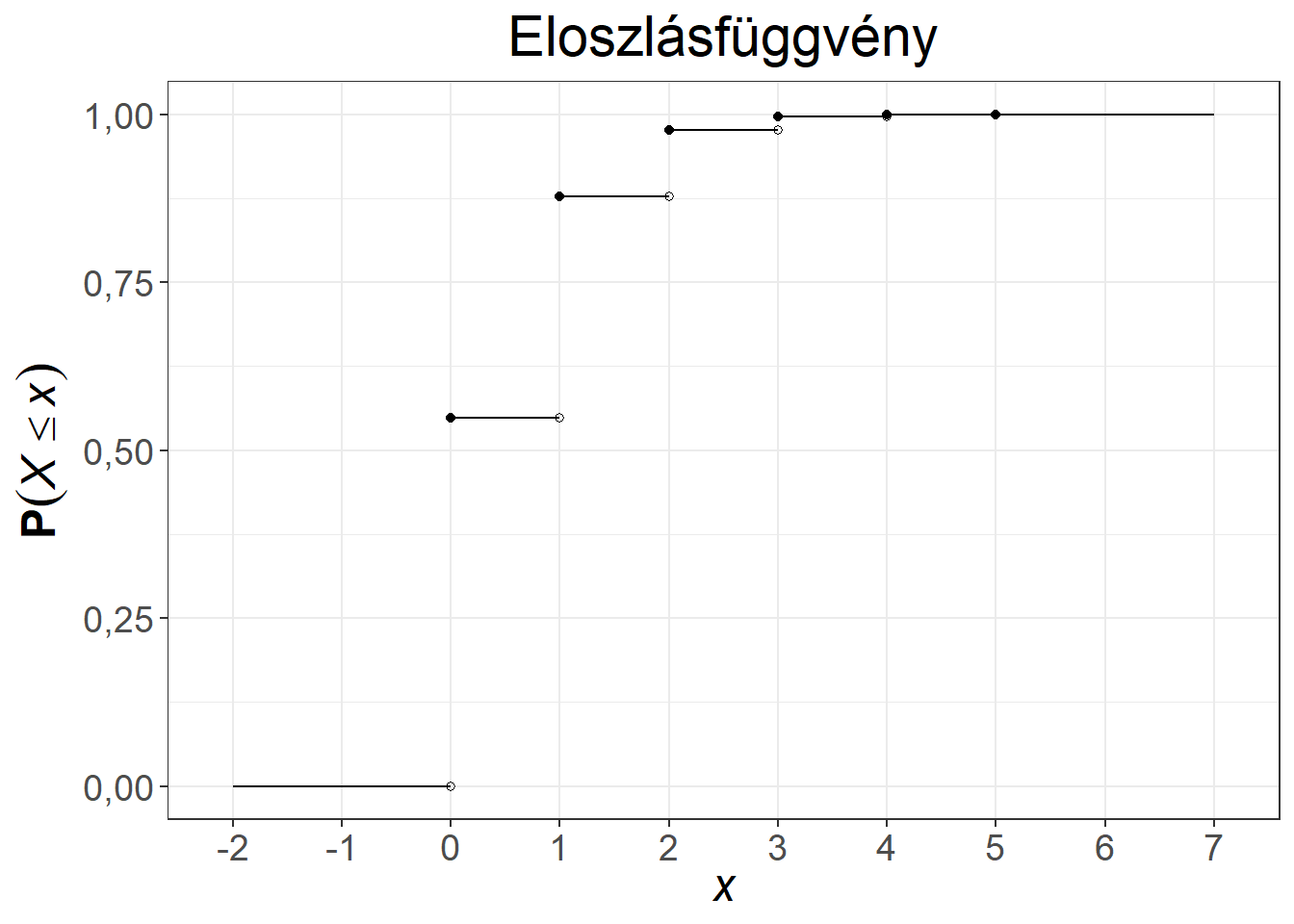
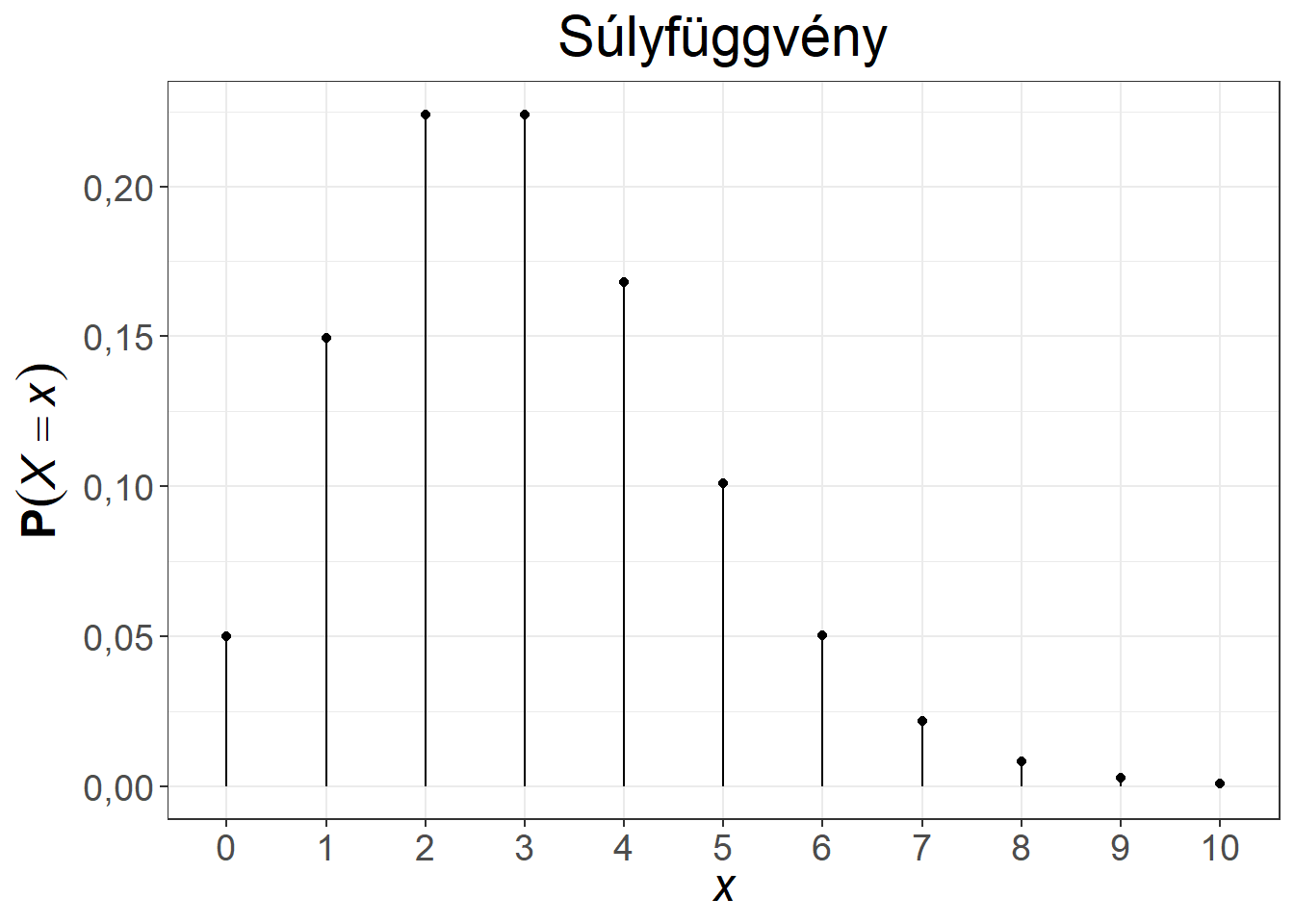
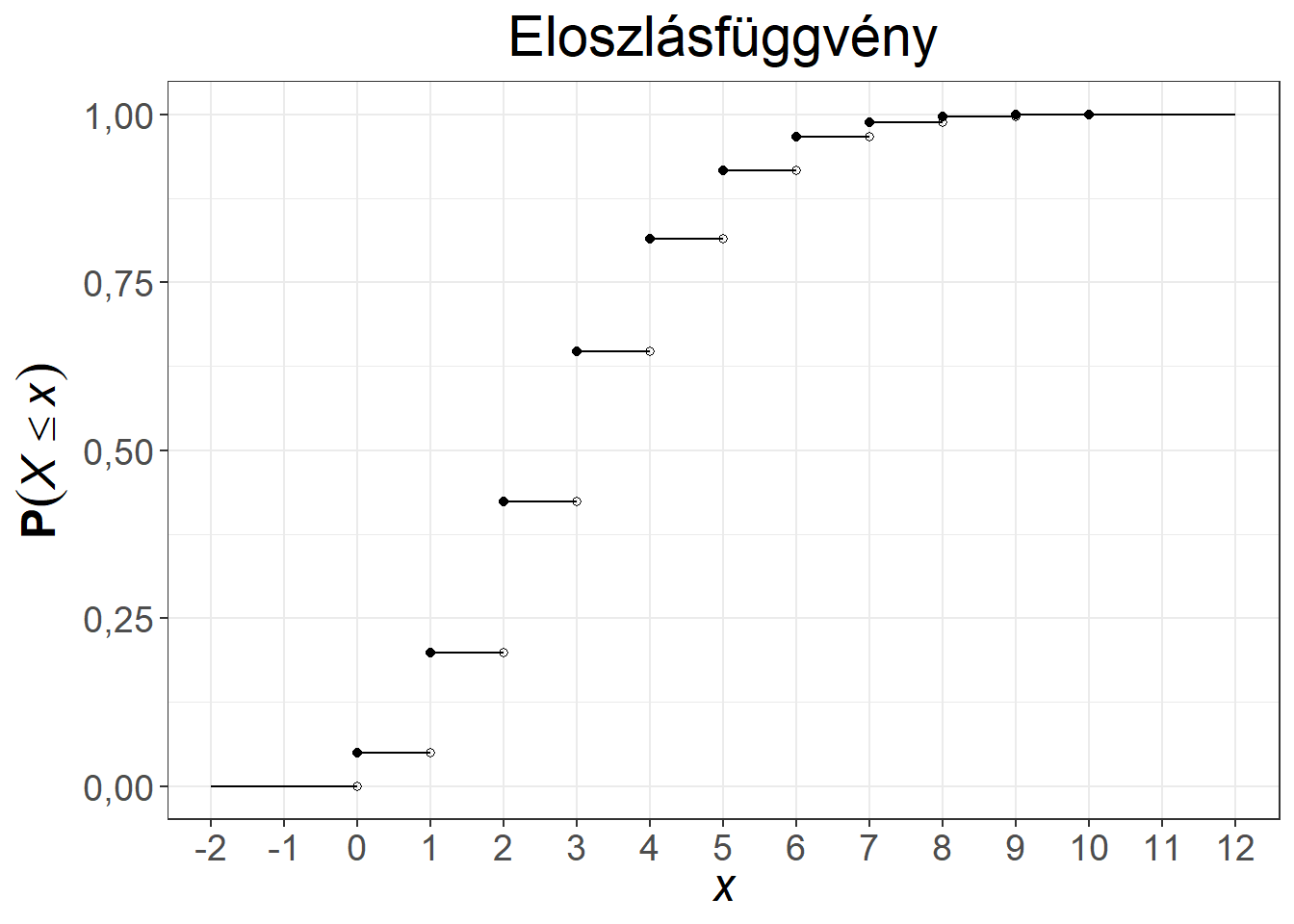
Ábra 5.5: A Poisson-eloszlás súly- és eloszlásfüggvénye, \(\lambda = 0,6\), illetve \(\lambda = 3\)
Amennyiben \(X_1\sim\text{Poi}(\lambda_1)\) és \(X_2\sim\text{Poi}(\lambda_2)\), akkor bizonyítható, hogy az \(X_1 + X_2\) valószínűségi változó szintén Poisson eloszlást követ, méghozzá \(\lambda_1 + \lambda_2\) paraméterrel, ami nagyban megkönnyíti az eloszlás alkalmazhatóságát. A fentiek természetesen nem csak két, hanem több eloszlás összegére is igazak.