4.1 Valószínűségszámítás alapfogalmai

A társadalmi, gazdasági, természeti jelenségek véletlen jellegük alapján az alábbi csoportokba sorolhatók.

4.1.1 Jelenségek csoportosítása

• determinisztikus
• sztochasztikus (véletlen jelenség)
  • egyszeri véletlen jelenség
  • véletlen tömegjelenség

A determinisztikus jelenségről beszélünk, ha adott körülmények mellett minden esetben ugyanaz az esemény következik be. Amennyiben adott körülmények között nem mindig azonos esemény következik be, a jelenséget sztochasztikusnak nevezzük. A két nagy csoport között nem annyira éles a határvonal, mint azt elsőre gondolnánk: azt, hogy egy jelenséget melyik csoportba sorolunk, nagyban befolyásolja, hogy mik azok az említett "adott körülmények".

A determinisztikus jelenségek leginkább a természettudományokat jellemzik. Amennyiben a megfelelő körülmények fennállnak (légnyomás, hőmérséklet, stb.), a jég elolvad. Ezzel szemben, amikor egy pénzérmét feldobunk, az hol a fej, hol az írás oldalával felfelé fog leesni. Ilyen szempontból a pénzérme feldobása sztochasztikus jellegű. Amennyiben lenne egy pénzfeldobó gépünk, ami figyelembe veszi az érme fizikai jellemzőit, a légmozgást, stb, úgy a jelenség többé már nem lenne sztochasztikus. Egy jelenség jellege tehát nagyban függ attól, hogy ésszerű kereteken belül mennyire tudjuk a körülményeket kontrollálni.

A sztochasztikus jelenségek még két csoportra bonthatók, az egyszeri véletlen jelenségek jellemzője, hogy az őket befolyásoló körülmények nem ismételhetők meg, míg a véletlen tömegjelenségek olyan jelenségek csoportját alkotják, amelyek -- legalábbis elvileg -- változatlan körülmények között akár végtelen sokszor megismételhetők. A valószínűségszámítás a fenti két csoport közül az egyszeri véletlen jelenségekkel nem foglalkozik, további vizsgálatainkban a véletlen tömegjelenségek vizsgálatára fókuszálunk.

Egyszeri véletlen jelenségek közé soroljuk például a sporteseményeket, amik jellemzően olyanok, hogy azonos körülmények között nem ismételhető meg, valószínűleg pontosan ez adja a sportfogadás népszerűségét. A véletlen tömegjelenségek közé tartozik például az egyszerű kockadobástól a lottóhúzáson át a statisztikai mintavétel is.

A statisztikai alkalmazásokon kívül a véletlen jelenségek és azok kezelése a gazdasági élet rengeteg területén felmerül. A pénzügyi élet, a biztosítótársaságok mind alkalmaznak valószínűségszámításon alapuló modelleket és módszereket. A következő három fejezetben olvasható ismeretek mindegyik témakör szempontjából hasznos ismeretek.

4.1.2 Elemi esemény, esemény, eseménytér

A véletlen jelenségek (más szóval véletlen kísérletek) során megfigyelünk egy kimenetelt, melyeket elemi eseményeknek hívunk, az elemi eseményeket \(\omega\) jelöli. Az összes elemi eseményt tartalmazó halmazt eseménytérnek nevezzük és \(\Omega\)-val jelöljük. A gyakorlatban jellemzően közvetlenül nem az elemi eseményekkel foglalkozunk, hanem eseményeket szeretnénk vizsgálni. Az események az elemi események egy részhalmazaként definiáljuk, és jellemzően az ABC elejéről származó nagybetűkkel jelöljük őket: \(A, B, C, \dots\), vagy amennyiben sok eseményről beszélünk, gyakran indexekkel különböztetjük meg őket: \(A_1, A_2, A_3, \dots\). Egy esemény tehát állhat 0, 1, vagy akár több elemi eseményből is. Azt az eseményt, ami 0 elemi eseményből áll (üres halmaz, jele \(\varnothing\)), lehetetlen eseménynek nevezzük. Az \(\Omega\) halmaz is egy esemény, ezt az eseményt biztos eseménynek nevezzük. Végül az adott kísérlethez tartozó események halmazát \(\mathcal{A}\) jelöli.

Már itt bevezetjük a valószínűség jelölését, a tananyagban \(\mathbf{P}()\) fogja jelölni egy adott esemény valószínűségét. A valószínűség tehát minden eseményhez egy számot rendel.

Tekintsük át a fenti fogalmakat és jelöléseket a kockadobás példáján!

• elemi esemény: a dobható számok, \(\omega_1=1\), \(\omega_2=2\), \(\dots\), \(\omega_6=6\)

• eseménytér: \(\Omega=\{\omega_i:i=1,2,3,4,5,6\} = \{1,2,3,4,5,6\}\)

• esemény:

  • \(A\): páros dobás, \(A=\{\omega_2,\omega_4,\omega_6\}=\{2,4,6\}\)
  • \(B\): páratlan dobás, \(B=\{\omega_1,\omega_3,\omega_5\}=\{1,3,5\}\)

• események halmaza:

  \(\mathcal{A}=\big\{\{\varnothing\},\{1\},\{2\},\dots,\{1,2\},\{1,3\},\dots,\{1,2,3\},\dots, \{\Omega\}\big\}\)

• valószínűség: \(\mathbf{P}(A) = \mathbf{P}(B) = 0{,}5\)

Természetesen a páros és páratlan dobás esetén jelen tananyag szerint még nem tudjuk, hogy a valószínűség 0,5 értéket vesz fel, de korábbi ismereteinkből ezt már felírhatjuk, feltételezve a kocka szabályosságát.

4.1.3 Események közti műveletek

Az események között definiálhatóak műveletek, illetve bemutatunk olyan jelöléseket, melyek eseményekhez kapcsolódnak. Legyen \(A, B \in \mathcal{A}\), azaz tartozzon mindkét esemény egy adott eseménytérhez.

• Azt az eseményt, amikor \(A\) és \(B\) esemény is bekövetkezik, a két esemény szorzatának, vagy a két esemény metszetének hívjuk és \(A \cap B\) módon jelöljük.
• Azt az eseményt, amikor az \(A\) és \(B\) események közül legalább az egyik bekövetkezik, a két esemény összegének, vagy a két esemény uniójának hívjuk és \(A \cup B\) módon jelöljük.
• Azt az eseményt, amikor nem az \(A\) esemény következik be, az \(A\) esemény \(\Omega\)-ra vett komplementer eseményének hívjuk és \(\overline{A}\) módon jelöljük.
• Ha \(A\) és \(B\) esemény olyan, hogy valahányszor \(A\) bekövetkezik, akkor \(B\) is, akkor \(A\)-ból következik \(B\) és \(A \subset B\) (vagy \(A \subseteq B\)) módon jelöljük. Amennyiben a két esemény egyezőségét is megengedjük, a \(A \subseteq B\) jelölést használjuk.
• Azt az eseményt, amikor \(A\) bekövetkezik, de \(B\) nem, a két esemény különbségének hívjuk és \(A-B\) (vagy \(A\cap \overline{B}\)) módon jelöljük.

Legyenek adottak az alábbi események:

• \(A=\{\text{páros dobás}\}\)
• \(B=\{5\text{-nél kisebb dobás}\}\)
• \(C=\{3\text{-nál kisebb dobás}\}\)

Ekkor

• \(A\cap B=\{2,4\}\)
• \(A\cup B=\{1,2,3,4,6\}\)
• \(\overline{A}=\{1,3,5\}\)
• \(C\subseteq B\) teljesül
• \(A\cap \overline{B} = \{6\}\)

Az eseményeket gyakran ábrázoljuk Venn diagram segítségével. Az összegzés és a szorzás műveletét mutatja be a 4.1. ábra.

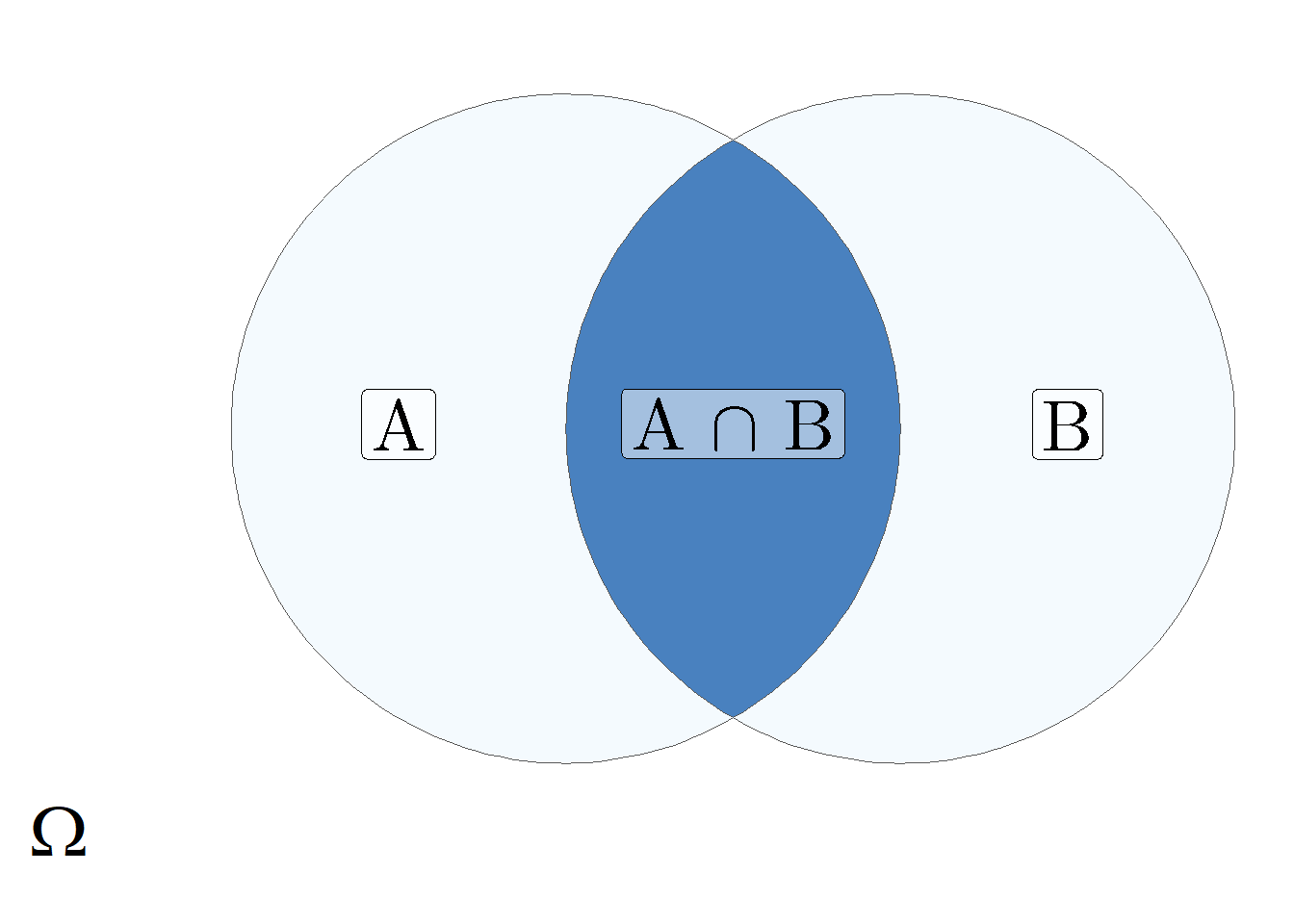
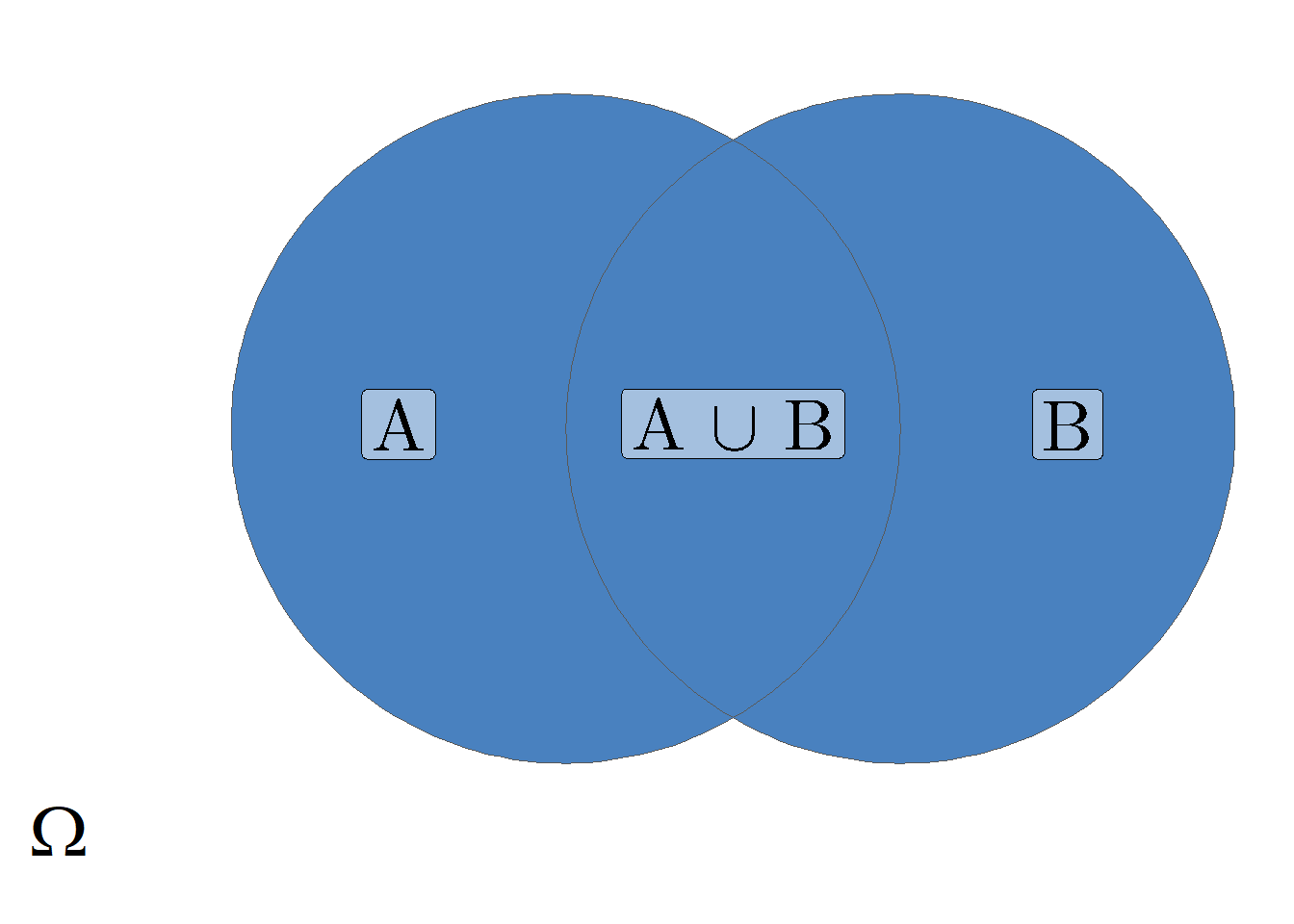
Ábra 4.1: Az összegzés és a szorzás művelete

A fenti műveletekkel és jelölésekkel kapcsolatosan néhány egyszerű szabály, összefüggés írható fel. Mind az események összege, mind pedig az események szorzata rendelkezik az idempotencia, kommutativitás, asszociativitás és disztributivitás tulajdonságával:

Táblázat 4.1: Az összegzés és szorzás tulajdonságai

tulajdonság	összeg	szorzat
idempotencia	\(A\cup A=A\)	\(A\cap A=A\)
kommutativitás	\(A\cup B=B\cup A\)	\(A\cap B=B\cap A\)
asszociativitás	\((A\cup B)\cup C=A\cup(B\cup C)\)	\((A\cap B)\cap C=A\cap(B\cap C)\)
disztributivitás	\(A\cap(B\cup C)=(A\cap B)\cup (A\cap C)\)	\(A\cup(B\cap C)=(A\cup B)\cap (A\cup C)\)

Az \(A\) esemény és annak \(\overline{A}\) komplementer eseményére vonatkozóan belátható, hogy

\[ A \cap \overline{A} = \varnothing \qquad A \cup \overline{A} = \Omega \]

azaz tetszőleges \(A\) esemény és komplementere egyszerre soha nem következnek be, illetve az \(A\) esemény és komplementere együttesen az eseményteret adják.

Szintén az események közötti elemi műveletekkel kapcsolatosak a DeMorgan azonosságok, melyek szerint tetszőleges \(A\) és \(B\) eseményekre igaz:

\[ \overline{A\cup B}=\overline{A}\cap\overline{B} \qquad \overline{A\cap B}=\overline{A}\cup\overline{B} \]

A fenti két azonosság Venn-diagram segítségével egyszerűen ellenőrizhető.

Az események egy \(A_1, A_2, \dots, A_n\) rendszerét teljes eseményrendszernek hívjuk, amennyiben az alábbi két feltétel teljesül:

\[\begin{equation} A_1 \cup A_2 \cup \dots A_n = \Omega \tag{4.1} \end{equation}\]

azaz az események összege a teljes eseményrendszer, valamint

\[\begin{equation} A_i \cap A_j = \varnothing \text{ minden } i \neq j, i,j = 1,2,\dots,n \text{-re} \tag{4.2} \end{equation}\]