7.2 Kétváltozós folytonos eloszlások

Kétváltozós folytonos eloszlásokról jelen tananyagban részletesen nem lesz szó, azonban a később tanult módszerek miatt elengedhetetlen egy rövid betekintés. Kétváltozós esetben a sűrűségfüggvényt egy görbe helyett egy felület írja le. Ahogy az egyváltozós esetben a görbe alatti terület, úgy kétváltozós esetben a felület alatti térfogat írja le az adott eseményhez tartozó valószínűséget. Az egyváltozós eset analógiájára a sűrűségfüggvény alatti térfogat egységnyi.

Az eloszlásfüggvény szintén egy monoton növekvő felületként képzelhető el, határértéke dél-nyugati irányban (ahol a két változó kis értékei szerepelnek) 0, észak-keleti irányban 1.

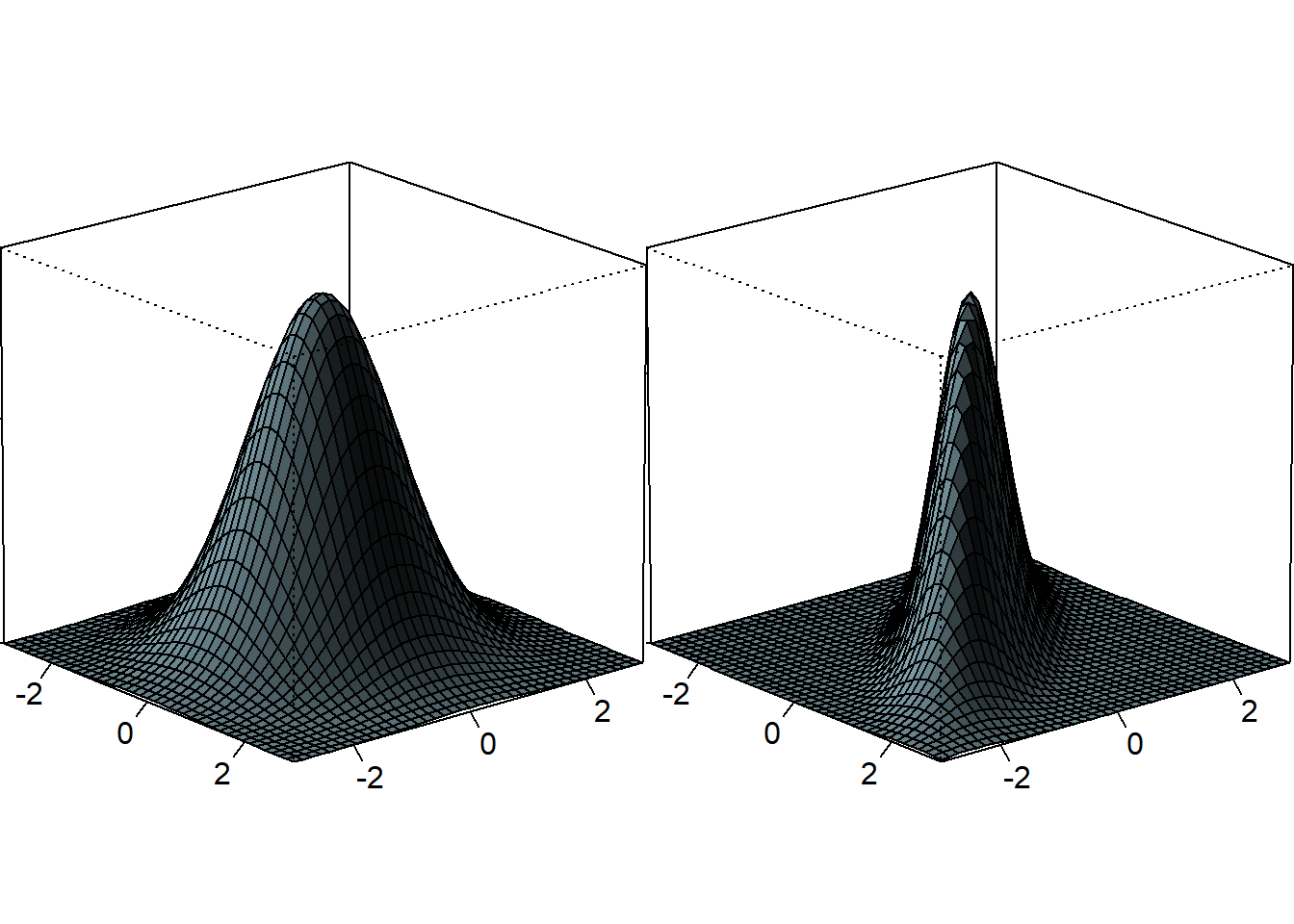
Az egyváltozós esethez hasonlóan a többváltozós valószínűségi változók esetén is beszélhetünk nevezetes eloszlásokról, és a többváltozós normális eloszlás a leggyakrabban alkalmazott eloszlások közé tartozik. A 7.2. ábra két különböző, kétváltozós normális eloszlás sűrűségfüggvényét mutatja be. Mindkét eloszlás várható érték vektora \([0, 0]\), a varianciák pedig minden esetben egységnyiek. A különbség a kétváltozós normális eloszlás fontos paramétere, a korrelációs együttható. A baloldali ábrán 0, míg a jobboldali sűrűségfüggvény esetén \(-0{,}8\) az értéke.

Ábra 7.2: Kétváltozós sűrűségfüggvény