3.4 Koncentráció

A koncentráció szó ismert köznapi jelentéssel bír, statisztikában azonban a koncentrációs vizsgálat a sokaság egyedeinek részesülését elemzi valamilyen változó alapján. A koncentráció elemezhető az egyedi megfigyelések alapján is, de jóval elterjedtebb annak vizsgálata a gyakorisági táblázat további elemzése kapcsán. Az elemzéshez szükségünk lesz a kumulált relatív gyakoriság mellett a kumulált relatív értékösszeg fogalmának bevezetésére.

3.4.1 Koncentrációs táblázat

Egy osztályközhöz tartozó értékösszeg alatt egyszerűen az abba az osztályba eső megfigyelések adott változó szerinti összegét értjük. Amennyiben az alapadatokat ismerjük, ez pontosan számítható egy egyszerű összegként, de gyakran élünk az alábbi közelítő meghatározással:

\[\begin{equation} S_j=F_j X_j^* \tag{3.5} \end{equation}\]

ahol \(F_j\) a \(j\). csoport gyakorisága, \(X_j^*\) az ún. osztályközép, az az érték, ami az adott osztályközt leginkább jellemzi, félúton az alsó és a felső határ között. Innen a relatív értékösszeg kiszámítása logikusan:

\[\begin{equation} Z_j=\frac{S_j}{\sum_{k=1}^J S_k} \tag{3.6} \end{equation}\]

ahol \(J\) az osztályközök száma. A kumulálás fogalmát már megismertük, a művelet mind az értékösszegre, mind a relatív értékösszegre elvégezhető, eredményül a kumulált értékösszeget (\(S_j^\prime\)) és a kumulált relatív értékösszeget (\(Z_j^\prime\)) kapjuk.

A TOP100 vállat márkaértékére vonatkozó további elemzéseket az alábbi táblázat tartalmazza:

Táblázat 3.5: Értékösszegek a TOP100 adatok alapján
osztályköz \(X_j^*\) \(F_j\) \(S_j\) \(S_j^\prime\) \(Z_j\) \(Z_j^\prime\)
-40] 20 74 1480 1480 0,333 0,333
(40-80] 60 13 780 2260 0,176 0,509
(80-120] 100 5 500 2760 0,113 0,622
(120-160] 140 2 280 3040 0,063 0,685
(160-200] 180 2 360 3400 0,081 0,766
(200-240] 220 2 440 3840 0,099 0,865
(240-280] 260 0 0 3840 0,000 0,865
(280- 300 2 600 4440 0,135 1,000
összesen - 100 4440 - 1,000 -
Az \(S_j\) közelítő értékösszeg szerint az első osztályközbe tartozó (40 milliárd dollár érték alatti) cégek összesen 1480 milliárd dolláros márkaértékkel rendelkeznek (ne feledjük, hogy ez egy közelítő érték, a tényleges összérték 1591,3 milliárd dollár, amit a nyers adatok ismeretében ebben a példában ki tudunk számítani), míg a második osztályközbe tartozók 780 milliárdos összértékkel. Ez a 4440 milliárdra becsült összérték 17,6%-át teszi ki. A \(Z_j^\prime\) oszlop harmadik sora például azt jelenti, hogy a 120 milliárd dollár alatti márkaértékek a teljes márkaérték mintegy 62,2%-át teszik ki.

A koncentráció elemzéséhez a kumulált relatív gyakoriság (\(G_j^\prime\)), valamint a kumulált relatív értékösszeg (\(Z_j^\prime\)) mutatóira van szükségünk, tulajdonképpen ezt a két számsort hasonlítjuk össze. A koncentrációs táblázat sematikus felépítése a 3.6. táblázatban látható. Az utolsó sorban természetesen mindkét kumulált sor esetén 1 érték szerepel, azaz a sokaság egésze felöleli az értékösszeg egészét.

Táblázat 3.6: Koncentrációs táblázat
osztályköz \(G_j^\prime\) \(Z_j^\prime\)
\(\left(X_1^{\text{alsó}}\right)\) - \(X_1^{\text{felső}}\) \(G_1^\prime\) \(Z_1^\prime\)
\(X_2^{\text{alsó}}\) - \(X_2^{\text{felső}}\) \(G_2^\prime\) \(Z_2^\prime\)
\(\dots\) \(\dots\) \(\dots\)
\(X_J^{\text{alsó}}\) - \(\left(X_J^{\text{felső}}\right)\) 1,000 1,000

A TOP100 márkaértékre vonatkozó koncentrációs táblázat az alábbi.

Táblázat 3.7: Koncentrációs táblázat a TOP100 adatok alapján
osztályköz \(G_j^\prime\) \(Z_j^\prime\)
-40] 0,740 0,333
(40-80] 0,870 0,509
(80-120] 0,920 0,622
(120-160] 0,940 0,685
(160-200] 0,960 0,766
(200-240] 0,980 0,865
(240-280] 0,980 0,865
(280- 1,000 1,000
A 3.7. táblázat alapján például azt olvashatjuk le, hogy a legkisebb márkaértékkel rendelkező vállalatok 87%-a a teljes márkaérték 50,9%-ával rendelkezik, vagy a vállalatok 98%-a az összérték 86,5%-ával, azaz a két legnagyobb márkaértékű vállalat rendelkezik a maradék 13,5%-kal. Vegyük észre, hogy két osztályköz esetén is azonosak a \(G_j^\prime\) és természetesen a \(Z_j^\prime\) értékek, ami azért következett be, mert üres osztályköz figyelhető meg az osztályközös gyakorisági sorban.

3.4.2 Lorenz-görbe

A Lorenz-görbe tulajdonképp a koncentrációs táblázat vizuális megjelenítését szolgálja egy pontdiagram segítségével. A vízszintes tengelyre a kumulált relatív gyakoriság, míg a függőlegesre a kumulált relatív értékösszeg kerül, az egyes pontok a gyakorisági táblából kerülnek ábrázolásra, majd összekötésre. Amennyiben nem lenne koncentráció, valamennyi pont a főátlón helyezkedne el, ezért a főátlót mintegy referenciaként ábrázolni szokás. A 3.8. ábra három különböző sokaságra vonatkozó görbét mutat be, rendre alacsony, közepes és magas koncentrációval.

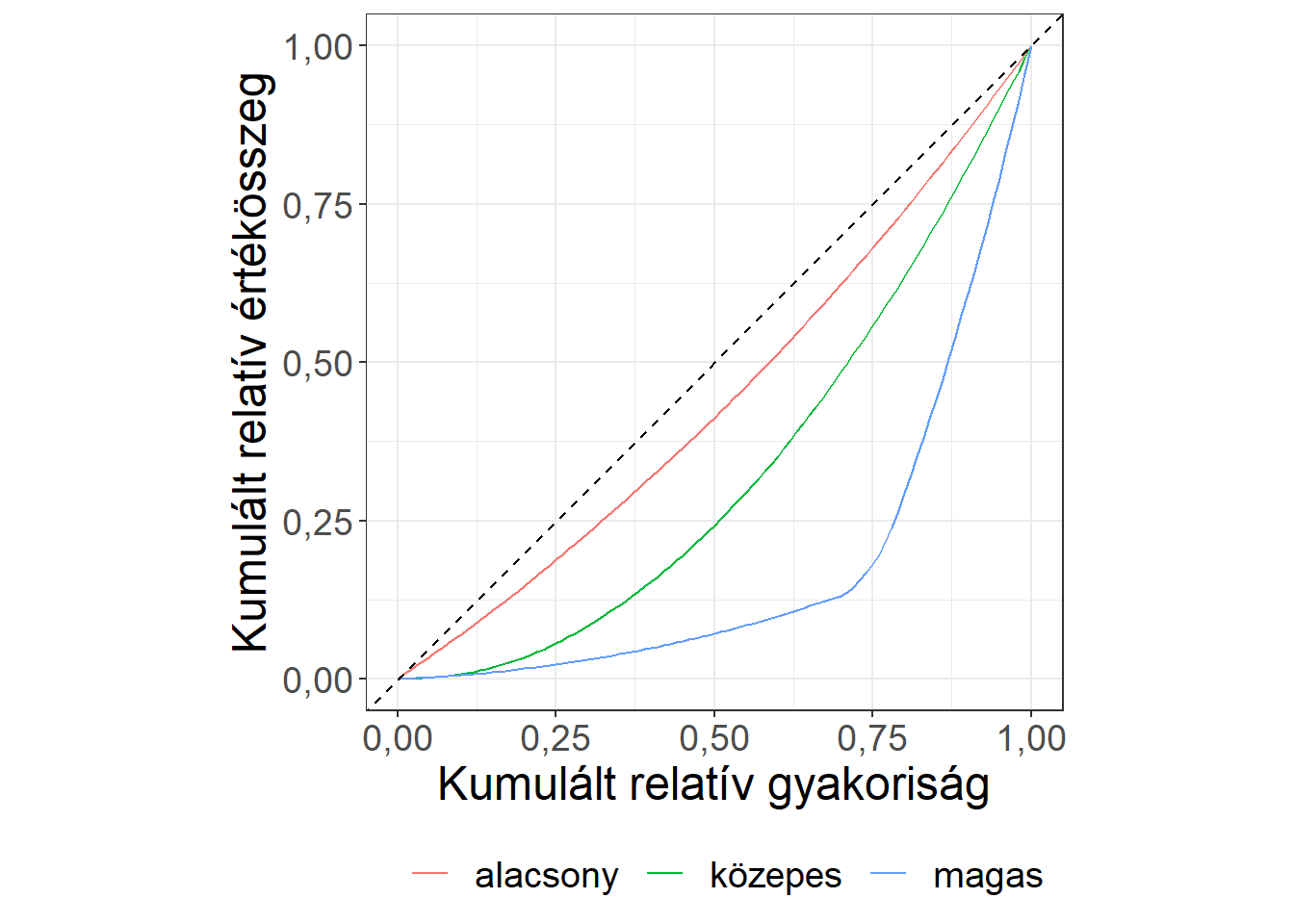
Három különböző Lorenz-görbe

Ábra 3.8: Három különböző Lorenz-görbe

A TOP100 márkaértékre vonatkozó (egyedi megfigyelések alapján készített) Lorenz-görbét mutatja be a 3.9. ábra. A koncentráció az ábra alapján is magasnak mondható.
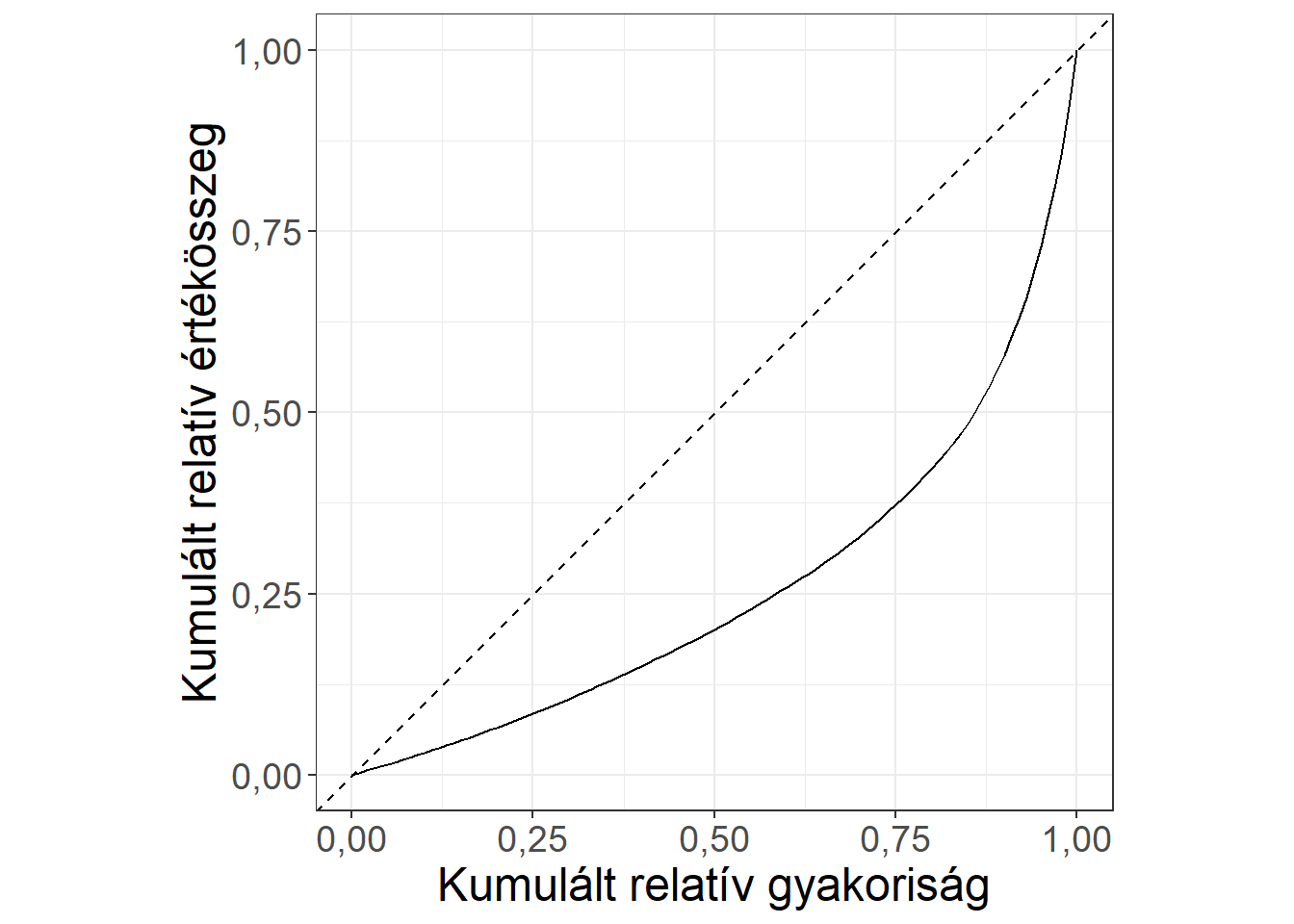
Lorenz-görbe a TOP100 márkaérték alapján

Ábra 3.9: Lorenz-görbe a TOP100 márkaérték alapján

A Lorenz-görbe esetén tehát minél messzebb fekszik a görbe az átlótól, annál erősebb a koncentráció. A Gini-együttható a görbe és az átló által bezárt terület nagyságát méri, a maximális 0,5-höz viszonyítva. A Gini-együttható értéke 0 és 1 közé normalizált, 0 értéke a koncentráció hiányát, 1 értéke a maximális koncentrációt mutatja.

A TOP100 márkaértékre vonatkozó Gini-index meghatározása meghaladja tananyagunk kereteit, értéke megközelíti a 0,5-öt, azaz elég erős koncentrációról beszélhetünk, még akkor is, ha csak a TOP100 márkaérték esetét vizsgáljuk. Ha a világ valamennyi márkáját tudnánk vizsgálni, a koncentráció még nagyobb lenne.

A koncentráció az egyedi adatok alapján is vizsgálható, ebben az esetben a relatív gyakoriságokat \(\frac{1}{N}\) adja minden megfigyelésre, míg a kumulált értékösszeget egyszerűen a növekvő rendbe állított megfigyelések kumulálásával kapjuk. Az egyedi adatokból készített Lorenz-görbe megrajzolását az érdeklődő Olvasóra bízzuk.