8.3 A Student t eloszlás
Az átlag mintavételi eloszlásáról elegendően nagy, \(n\) elemű minta esetén azt találtuk a (8.4) összefüggésben, hogy a
\[ Z = \dfrac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}} \sim \mathcal{N}\left(0,1\right) \]
valószínűségi változó standard normális eloszlást követ. A valószínűségi változóban a véletlen elem az \(\overline{X}\) változóban rejlik, hisz a mintaátlag mintáról mintára eltérő lehet. A centrális határeloszlás tétel miatt ez a standardizált eredmény széles körben használható. Sok gyakorlati esetben azonban a \(\sigma\) sokasági szórás ismeretlen, így az összefüggés közvetlenül nem használható. Ilyen körülmények között természetes gondolat, hogy \(\sigma\) helyett a mintabeli korrigált szórást alkalmazzuk a képletben, azaz a
\[\begin{equation} T = \dfrac{\overline{X}-\mu}{\frac{S}{\sqrt{n}}} \sim \sim {}_{n-1} t \tag{8.12} \end{equation}\]
valószínűségi változót kell alkalmaznunk. Ez a valószínűségi változó már nem standard normális eloszlású, illetve a mintabeli átlag mellett a mintabeli szórás is megjelenik, mint valószínűségi változó. A \(T\) valószínűségi változót Student t eloszlásúnak nevezzük, aminek szintén egy paramétere van (\(\nu\)) és szintén szabadságfoknak nevezzük.8
A Student t eloszlás nevét nem egy hallgatóról, vagy egy Student nevű tudósról kapta. Az eloszláshoz kapcsolódó matematikai problémát William Sealy Gosset publikálta Student álnéven, aki a Guinness sörfőzde alkalmazásában állt. Az eloszlás kvantiliseit tartalmazó táblázatot azzal a kommenttel küldte el a 20. század talán legnagyobb hatású statisztikusának, Ronald Fishernek, hogy talán Fisher az egyetlen ember a világon, aki azt használni fogja a megalkotóján kívül. Ennél nagyobbat nehezen tévedhetett volna.
A t eloszlás tehát figyelembe veszi azt a többlet bizonytalanságot is a mintavétel során, hogy adott esetben nem csak a sokasági átlag, hanem a sokasági variancia is ismeretlen. Az eloszlás alakja ettől függetlenül nagyon hasonlít a standard normális eloszláséra, szimmetrikus, azonban az eloszlás farkaiban nagyobb, míg a várható érték körül relatíve kisebb a sűrűségfüggvény értéke. A \(\nu\) szabadságfokú t eloszlás momentumai:
\[\begin{equation} \mathbf{E}(X)=0 \left(\nu>1\right), \quad \mathbf{D}^2(X)=\frac{\nu}{\nu-2} \left(\nu>2\right) \tag{8.13} \end{equation}\] azaz a standard normális eloszláshoz hasonlóan a várható érték 0, a variancia azonban egynél nagyobb, ami pontosan a többlet bizonytalanságot testesíti meg. \(\nu = 1\) esetén a \(\mathbf{E}(X)\) várható érték nem létezik, valamint \(\nu \leq 2\) esetén \(\mathbf{D}^2(X)\) sem létezik. A nem létező momentumok esetére jelen tananyagban nem tértünk ki részletesen, de a fentiek a nagyon kis minták esetén problémákat okoznak.
Az is megfigyelhető, hogy a szabadságfok (ami közvetlenül a mintalemszámhoz kapcsolódik) növekedésével a variancia egyre közelebb kerül felülről a standard normális eloszlás 1 értékéhez, hiszen az egyre nagyobb mintából egyre közelebb kerül a mintabeli és a sokasági szórás. Ugyanez figyelhető meg az eloszlások alakján is, a 8.4. ábrán a standard normális eloszlás és különböző szabadságfokú t eloszlások láthatók.
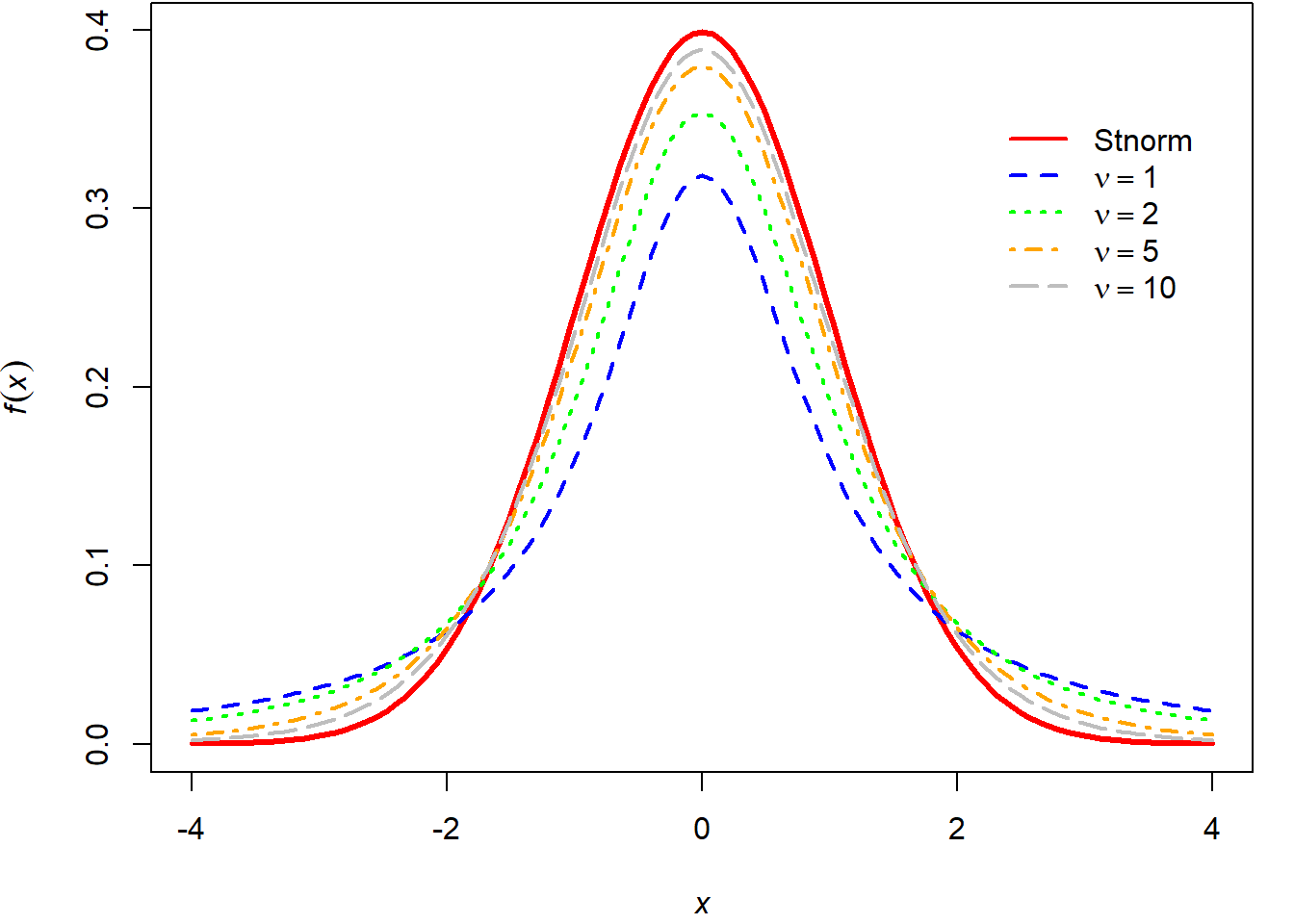
Ábra 8.4: A standard normális és különböző szabadságfokú t eloszlások
A t eloszlásból származó kvantilisek táblázata megtalálható a Képletgyűjteményben és természetesen szoftveres úton is meghatározhatók a szükséges értékek. Amennyiben különböző szabadságfokú t eloszlások és a standard normális eloszlás \(\alpha\) kvantiliseit (azokat az értékeket, melyektől \(\alpha\) terület van jobbra) hasonlítjuk össze, azt láthatjuk, hogy
- a t eloszlások kvantilisei magasabbak a standard normális értéknél,
- a szabadságfok növekedésével a t eloszlás kvantilisei a normális eloszlásból származó értékhez tartanak, azt minden határon túl megközelítik,
- a fentiek miatt nagy minta esetén tulajdonképpen a standard normális eloszlásból származó érték is használható a gyakorlatban.
Keressük meg a 8.4. ábrán látható t eloszlások esetére azokat a kvantiliseket, melyek 5-5%-ot vágnak le az eloszlás alján és tetején. A szimmetria miatt tudjuk, hogy minden szabadságfok mellett a két keresett érték egymás ellentéte, ezért elegendő az egyiket megkeresnünk. Szoftver, vagy a t eloszlás táblázata alapján azt kapjuk, hogy a keresett pozitív kvantilisek
| \(\nu\) | \({}_{\nu}t_{0{,}95}\) |
|---|---|
| 1 | 6,314 |
| 2 | 2,920 |
| 5 | 2,015 |
| 10 | 1,812 |
Azt látjuk, hogy ezek a kvantilisek egyre kisebbek, ami mögött az a tény húzódik meg, hogy nagyobb minta alapján becsült sokasági szórás esetén egyre kevésbé vagyunk bizonytalanok. A szabadságok növekedésével a kvantilisek a normális eloszlásból származó \(z_{0{,}95} = 1{,}645\) értékhez közelítenek.
A hasonlóság nem véletlen, a t eloszlás egy standard normális eloszlás és egy \(\chi^2\) eloszlás hányadosához kapcsolódik, emiatt azonos a paraméterek száma és elnevezése is.↩︎