6.1 Eloszlás- és sűrűségfüggvény

A fejezetben a folytonos valószínűségi változók jellemzésére szolgáló két eszközt, az eloszlásfüggvényt és a sűrűségfüggvényt mutatjuk be.

Egy \(X\) folytonos valószínűségi változó eloszlásfüggvénye alatt a

\[\begin{equation} F(x) = \mathbf{P} \left( X \leq x\right) \tag{6.1} \end{equation}\]

függvényt értjük, ami egy tetszőleges valós számhoz az \(X \leq x\) esemény bekövetkezési valószínűségét rendeli. Ahogy azt már említettük, a folytonos valószínűségi változók esetében a valószínűségek kiszámításához minden esetben az eloszlásfüggvényt fogjuk használni, ezért érdemes a lehetséges változatokat felsorolni:

• \(\mathbf{P} \left( X \leq a\right) = \mathbf{P} \left( X < a\right) = F(a)\)
• \(\mathbf{P} \left( X \geq a\right) = \mathbf{P} \left( X > a\right) = 1 - F(a)\)
• \(\mathbf{P} \left(a \leq X \leq b\right) = \mathbf{P} \left(a < X \leq b\right) = \mathbf{P} \left(a \leq X < b\right) = \mathbf{P} \left(a < X < b\right) = F(b) - F(a)\)

Amint az a fentiekből is látható, folytonos esetben az események esetén az egyenlőségek nem relevánsak, hiszen a definíció szerint az elemi események valószínűsége 0.

Az eloszlásfüggvény definíciójából adódóan az 0 és 1 közötti értéket vehet fel, monoton növekvő, folytonos függvény. Határértéke \(\lim_{x\to-\infty}F(x)=0\), illetve \(\lim_{x\to\infty}F(x)=1\).

Egy \(X\) folytonos valószínűségi változó sűrűségfüggvénye alatt az \(f\) függvényt értjük, ha

\[\begin{equation} F(x) = \int_{-\infty}^x f(u) \mathrm{d} u \tag{6.2} \end{equation}\]

amiből szokásos feltételek mellett következik, hogy

\[\begin{equation} f(x)=F'(x) \tag{6.3} \end{equation}\]

A sűrűségfüggvényre igaz, hogy \(f(x)\geq 0\), illetve \(\int_{-\infty}^\infty f(x) \mathrm{d}x=1\). A teljes görbe alatti terület tehát egységnyi, ami a valószínűséget reprezentálja. Fontos azonban hangsúlyozni, hogy a sűrűségfüggvény \(f(x)\) értéke nem valószínűségként értelmezendő, hanem csupán a valószínűség sűrűsödéséről ad képet. Matematikailag ez azt jelenti, hogy a sűrűségfüggvény \(x\) kis sugarú környezetében a valószínűség sűrűsödését írja le: \(\mathbf{P}(x<X<x+\Delta x)\approx f(x)\Delta x\).

A görbe alatti terület tehát egységnyi, a (zárt, vagy nyílt) intervallumba esés valószínűségét a sűrűségfüggvény segítségével integrál segítségével határozhatjuk meg, azaz \(\mathbf{P}(a<X<b)=\int_a^b f(x)\mathrm{d} x\).

A sűrűség- és eloszlásfüggvény -- hasonlóan a diszkrét eloszlásokhoz -- egyértelmű kapcsolatban van egymással. Ahogy diszkrét esetben összegzéssel, illetve kivonással meghatározható egyik függvényből a másik, úgy folytonos esetben az integrálás, illetve a deriválás művelete segít a meghatározásban.

A 6.2. ábrán egy egyszerű folytonos eloszlás sűrűségfüggvénye, illetve a hozzá tartozó eloszlásfüggvény látható. A valószínűségi változó \(-1\) és 1 közötti értékeket vehet fel, a legerősebb sűrűsödés az \(x = 0\) környékén látható, \(f(0) = 1\), de ez értelemszerűen nem jelenti azt, hogy a 0 értéket 1 valószínűséggel veszi fel a változó. A görbe alatti terület összesen egységnyi, ami egyszerű matematikai módszerekkel két háromszög területeként számítható ki. Az \(x=0\) ponttól balra eső görbe alatti terület a sűrűségfüggvény esetén 0,5, azaz \(\mathbf{P}(X \leq 0) = \int_{-\infty}^0 f(x) \mathrm{d}x=0{,}5\). Ugyanez a valószínűség olvasható le az eloszlásfüggvényről (jóval egyszerűbben), hiszen \(\mathbf{P}(X \leq 0) = F(0) = 0{,}5\).

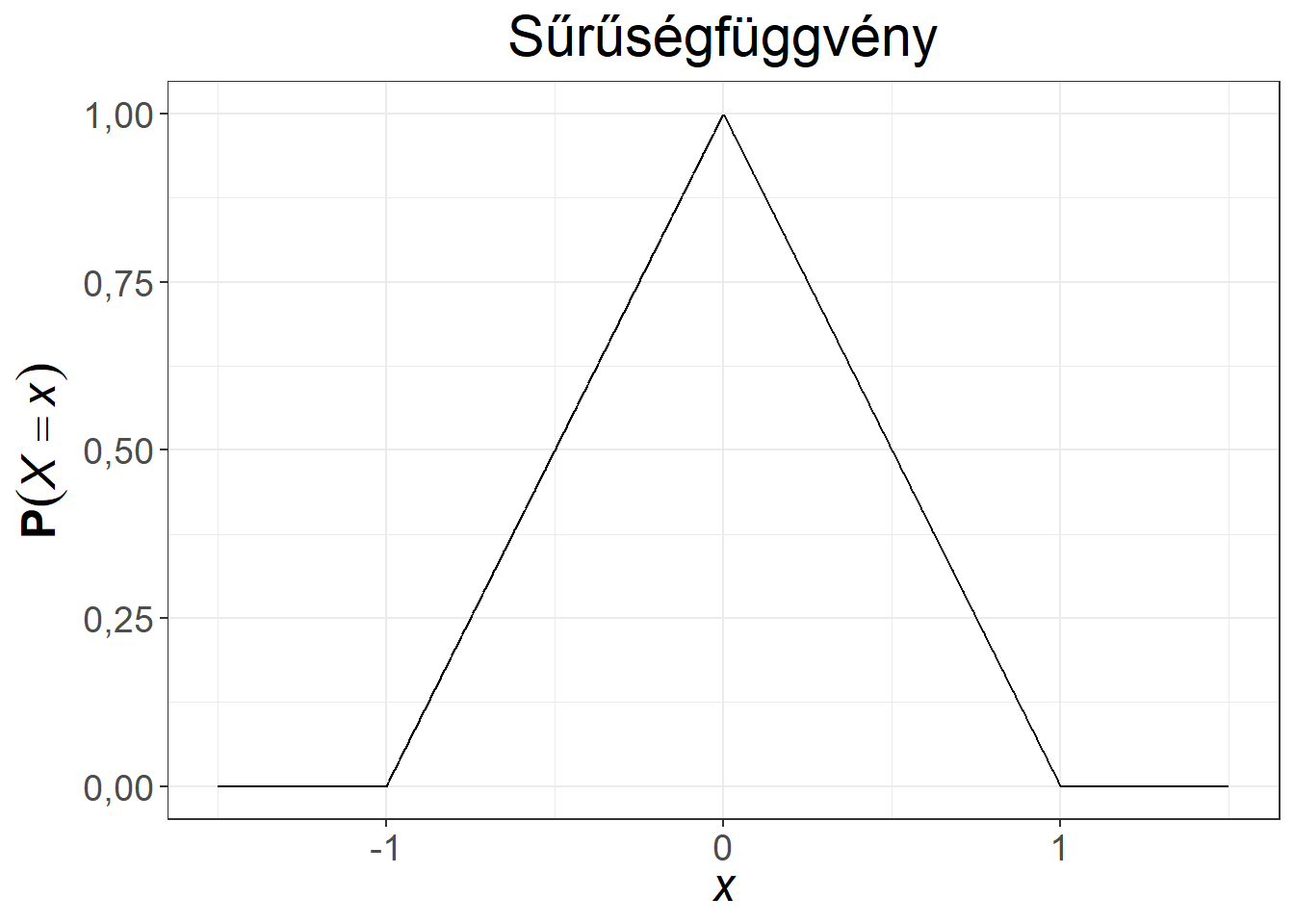
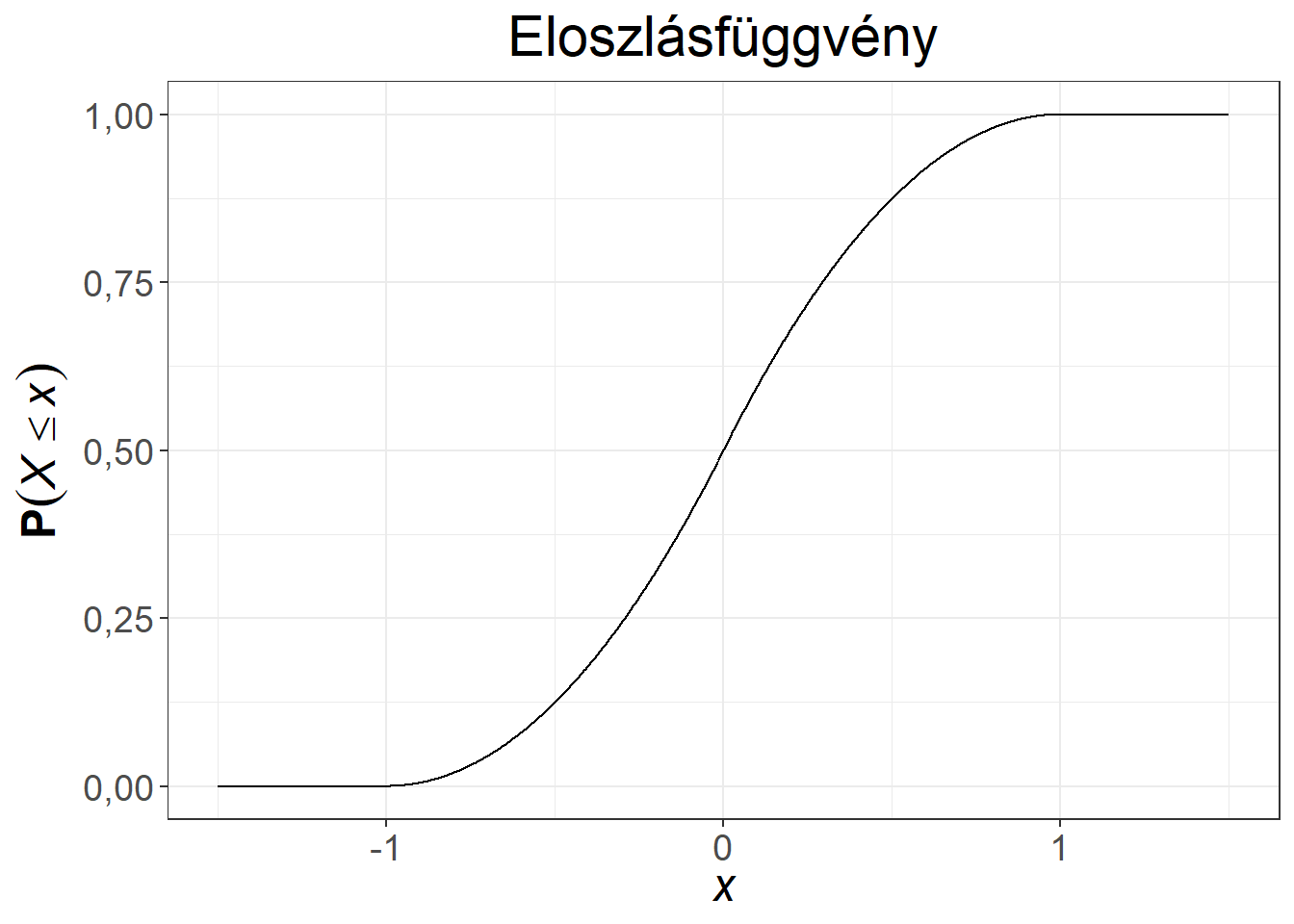
Ábra 6.2: Folytonos valószínűségi változó sűrűség- és eloszlásfüggvénye

Vegyük észre, hogy az eloszlásfüggvény folytonossága miatt a függvényérték bejárja a 0-1 intervallumot, azaz tetszőleges \(p\) valószínűséghez meghatározható az az \(x\) érték, melyre igaz, hogy \(F(x) = \mathbf{P} \left( X \leq x\right) = p\), ezt a kifejezést az eloszlásfüggvény inverzének hívjuk és \(x = F^{-1}(p)\) módon jelöljük. Az eloszlásfüggvény inverzének segítségével tehát adott \(p\) valószínűséghez tudjuk meghatározni azt az \(x\) értéket, melyhez pontosan a \(p\) eloszlásfüggvény-érték tartozik.