3.5 Gyakorló feladatok

Szükséges Excel ismeretek

Függvények:

  • kvantilisek:
    • KVARTILIS.KIZÁR, KVARTILIS.TARTALMAZ
    • PERCENTILIS.KIZÁR, PERCENTILIS.TARTALMAZ
  • osztályközös gyakorisági sor: GYAKORISÁG
A GYAKORISÁG egy ún. tömbfüggvény. Alkalmazásához előre ki kell jelölnünk azokat a cellákat ahova a gyakoriságokat meg szeretnénk kapni. A Csoport-tömbnek a kívánt osztályközök felső határait kell megadnunk, majd a függvényt az ENTER helyett a CTRL+SHIFT+ENTER billentyűkkel kell meghívni.
  • alakmutatók: FERDESÉG.P, CSÚCSOSSÁG
Az Excelben szerepel a FERDESÉG és a FERDESÉG.P függvény, amelyből a második az, ami a (3.3) formulával adott mérőszámot kiszámítja. A FERDESÉG függvény is hasonló eredményt ad, az a függvény a minta ferdeségéből enged következtetést levonni, ami a későbbi fejezetek tananyaga. Sajnos a csúcsosság esetén nem került implementálásra a sokasági adatokra alkalmazható függvény (nincs CSÚCSOSSÁG.P függvény), így a némileg eltérő, de implementált függvényt fogjuk használni, vállalva a kis pontatlanságot.

Funkciók:

  • Hisztogram és Doboz-diagram (boxplot) beszúrása
  • Adatelemzés menü Hisztogram eszköze
Az Excelbe beépített szabály általában túl sok osztályközt hoz létre, de lehetőség van az osztályközök számának módosítására. A 2016-os Excel verzióban már közvetlenül elérhető a hisztogram és a boxplot ábrája, és a hisztogram viszonylag rugalmasan testreszabható. Az Adatelemzés menü használatakor a Rekesztartomány opciónál megadhatjuk a kívánt osztályközök felső határait. A leginkább rugalmas megoldás (pl. eltérő hosszúságú osztályközök készítéséhez) természetesen a GYAKORISÁG tömbfüggvény alkalmazása.

Nyissa meg a hallgatok.xlsx fájlt és vizsgálja meg az összes jövedelem változóját!

  1. Jellemezze a változót az ún. five-number summary értékekkel! Értelmezze a kiszámított mutatókat! Milyen az átlag és a medián viszonya? Mit tud elmondani ezek alapján az eloszlás alakjáról?
    1. Számítsa ki az összes jövedelem változó intekvartilis terjedelmét!
    2. Melyik az az érték, amelynél a hallgatók 30 százalékának magasabb az összes jövedelme?
  2. Ábrázolja az előző feladatban kiszámított értékek alapján az eloszlás boxplotját! Hasonlítsa össze a férfi és női hallgatók jövedelmét boxplot diagrammokat felhasználva! Mit tud elmondani az adatokról az ábra alapján?
  1. Készítsen osztályközös gyakorisági sort a gyakoriság függvény segítségével! Számítsa ki és értelmezze az előadáson megismert mutatókat (kumulált gyakoriság, relatív gyakoriság, értékösszeg, stb.)!
  1. Készítsen hisztogramot az előző feladat adatai, illetve az Adatelemzés menü Hisztogram menüpontja segítségével is! Mik az előnyei-hátrányai az egyes megközelítéseknek?
  2. Számítsa ki a jövedelem változó csúcsosságát és ferdeségét! Mit mutatnak ezek a mutatók?
  1. Egy futball válogatott által 10 mérkőzésen kapott gólok a következők: 4, 1, 2, 1, 0, 8, 1, 3, 0, 0. Számítsa ki és értelmezze a mérkőzésenként kapott gólok kvartiliseit kézzel, majd ellenőrizze eredményeit Excellel! Mekkora az interkvartilis terjedelem?

Az eredményeket az alábbi táblázat foglalja össze. A különböző számítási módok némileg eltérő, de hasonló eredményt adnak.

mutató kézzel KVARTILIS.KIZÁR KVARTILIS.TARTALMAZ
alsó kvartilis 0 0 0,25
felső kvartilis 3 3,25 2,75
interkvartilis terjedelem 3 3,25 2,5
  1. Egy kisvállalat 12 dolgozójának életkora az alábbi: 34, 28, 29, 54, 43, 32, 55, 25, 37, 41, 44, 44. Számítsa ki és értelmezze az életkor kvartiliseit kézzel, majd ellenőrizze eredményeit Excellel!

Az eredményeket az alábbi táblázat foglalja össze. A különböző számítási módok némileg eltérő, de hasonló eredményt adnak.

mutató kézzel KVARTILIS.KIZÁR KVARTILIS.TARTALMAZ
alsó kvartilis 29 29,75 31,25
felső kvartilis 44 44 44
interkvartilis terjedelem 15 14,25 12,75
  1. Vizsgáljuk meg a hallgatok.xlsx fájl adatai alapján a sportra költött összeg eloszlásának jellemzőit!
    1. Számítsa ki a kvartiliseket és értelmezze őket!
    2. Mennyi a második kvintilis értéke! Értelmezze is azt!
    3. Számítsa ki az eloszlás csúcsosságát, illetve ferdeségét jellemző mutatót! Mit tapasztal?
    4. Készítsen hisztogramot! Tapasztalja az előző kérdésben levont következtetéseket az eloszlás alakjára vonatkozóan?
    5. Számítsa ki a hallgatók z-értékeit sportra költött összeg szempontjából! Melyik hallgatók a leginkább extrémek sportra költött összeg szempontjából?
  1. A feladat megoldásához a KVARTILIS.TARTALMAZ függvény használata javasolt.
mutató érték Excel függvény
MIN 0 =KVARTILIS.TARTALMAZ(sokaság;0)
Q1 0 =KVARTILIS.TARTALMAZ(sokaság;1)
Q2 = Me 2000 =KVARTILIS.TARTALMAZ(sokaság;2)
Q3 5000 =KVARTILIS.TARTALMAZ(sokaság;3)
MAX 26000 =KVARTILIS.TARTALMAZ(sokaság;4)

Értelmezések: A hallgatók minimálisan 0 Ft-ot költenek sportra. A hallgatók negyede legfeljebb 0 Ft-ot költ sportra. A hallgatók fele 2000 Ft-nál kevesebbet költ sportra. A hallgatók háromnegyede 5000 Ft-nál kevesebbet költ sportra. A hallgatók maximálisan 26000 Ft-ot költenek sportra.

  1. A második kvintilis értéke 1000, amely azt mutatja meg, hogy a hallgatók 2/5-öd része, azaz 40%-a legfeljebb 1000 Ft-ot költ sportra.

  2. A csúcsosság mutató értéke 6 (CSÚCSOSSÁG függvény használatával), ami azt mutatja, hogy az eloszlás alakja erősen csúcsos. A ferdeség mutató értéke pedig 2,153 (FERDESÉG.P függvény használatával), ami erős jobboldali aszimmetriára utal.

  3. Az alábbi hisztogram mutatja a megfigyelések gyakoriságát az egyes osztályközökben. A jobboldali aszimmetriát mutatja, hogy az eloszlás alakja jobbra hosszan elnyúló.

  1. A z-score értékeket úgy kapjuk meg ha a megfigyelésekből kivonjuk a sokasági átlagot, és a különbséget elosztjuk a sokasági szórással. A 267-es számú hallgató a legextrémebb a sportra költött összeg szempontjából, mivel abszolút értékben az ő z-értéke tér el leginkább a 0-tól (5,48).
  1. Nyissa meg az NBA.xlsx fájlt!
    1. Elemezze a játékosok testmagasságát a teljes sokaságban és pozíciók szerint is! Mit tapasztal?
    2. Készítsen hisztogramot a testmagasság, a játszott meccsek és az összes dobott pont változók alapján, több különböző osztályköz-hossz felhasználásával! Mit tud elmondani az eloszlások alakjáról? Megállapításait mutatókkal is támassza alá!
  1. Az átlagos magasságokat pozíciók szerint az alábbi táblázat foglalja össze. Ilyen táblázatot kapunk, ha az Excelben kimutatást készítünk, amelynek soraiban a "pozíció" szerepel, az értékek pedig a "magasság" változó átlagai
pozíció átlagmagasság (cm)
C 205,7
PF 209,3
PG 191,5
SF 203,8
SG 199,9
összesen 200,1
  1. A hisztogramokhoz először készítsünk osztályközös gyakorisági sorokat. Ehhez határozzunk meg osztályköz-határokat (testmagasságnál pl. 175, 180, 185, 190, 195, 200, 205, 210, 215, 220, 225, 230). Az osztályközök felső határait írjuk Excelben egy oszlopba. Ezen értékek mellett (a cellákat kijelölve) alkalmazzuk a =GYAKORISÁG(változó;osztályközhatárok) tömbfüggvényt és CTRL+SHIFT+ENTER billentyűkombinációval töltsük ki a cellákat. Az osztályközös gyakorisági sor a testmagasság esetén:
osztályköz gyakoriság
175 0
180 2
185 13
190 55
195 45
200 62
205 80
210 98
215 47
220 11
225 1
230 1
235 0

Az osztályközös gyakorisági sorból ezután oszlopdiagramot készíthetünk, ez lesz a hisztogram.

A különböző változók eloszlásának alakját leíró csúcsosság és ferdeség mutatókat az alábbi táblázat foglalja össze.

mutató magasság játszott meccsek összes pont
csúcsosság (CSÚCSOSSÁG) -0,697 -0,175 0,245
ferdeség (FERDESÉG.P) -0,199 -0,934 0,913

A "magasság" és a "játszott meccsek" változó eloszlása baloldali aszimmetriát mutat, és a normálisnál laposabb. Az "összes pont" változó jobboldali aszimmetriát mutat és a normálisnál csúcsosabb.

  1. Egy elemzésben öt sokaságot jellemeztünk a five number summary értékekkel, és ezeket sokaságonként boxplot segítségével ábrázoltuk. Adja meg, hogy melyik sorszámú sokaságra jellemzőek leginkább az alábbi állítások!
    1. Vélhetően ennek a sokasági eloszlásnak a legmagasabb a csúcsosság értéke.
    2. Vélhetően ez a sokasági eloszlás a leglapultabb.
    3. Ennek a sokaságnak a legnagyobb a terjedelme.
    4. Ennek a sokaságnak a legalacsonyabb az alsó kvartilise.
    5. Ennek a sokaságnak a mediánja 15.
    6. Ennek a sokaságnak a felső kvartilise 17.
    7. Ez a sokasági eloszlás jobboldali aszimmetriát mutat.
    8. Ez a sokasági eloszlás baloldali aszimmetriát mutat.
    9. Ennek a sokaságnak a legmagasabb a maximumértéke.
    10. Ennek a sokaságnak a minimumértéke 9.
    11. Vélhetően ennek a sokasági eloszlásnak erősen negatív a ferdeség értéke.
    12. Ebben a sokaságban az értékek 75%-a 14-nél nagyobb.
    13. Ebben a sokaságban az értékek 25%-a 6-nál kisebb.

A keresett sokaságok rendre: 4, 5, 4 (ha a ponttal jelzett kiugró értékeket is figyelembe vesszük a számításnál), 5, 1, 1, 2, 1, 3, 3, 1, 3, 5.

  1. Egy elemzésben öt különböző (A,B,C,D,E) sokaságot ábrázoltunk hisztogram segítségével. Adja meg, hogy melyik betűjellel ellátott sokaságra jellemzőek leginkább az alábbi állítások! Válaszolja meg az alábbi feladatokat!
    1. Ennek a sokaságnak az eloszlása a legcsúcsosabb.
    2. Ez a sokasági eloszlás jobboldali aszimmetriát mutat.
    3. Ez a sokasági eloszlás baloldali aszimmetriát mutat.
    4. Ennek a sokaságnak a legnagyobb a terjedelme.
    5. Vélhetően ennek a sokaságnak a legmagasabb az átlaga.
    6. Ennek a sokaságnak a hisztogramján nem látható 10 feletti gyakoriságú osztályköz.
    7. Ennek a sokaságnak a hisztogramja két olyan osztályközt is mutat, amelyekben 20-nál több megfigyelés található.
    8. Ebben a sokaságban pontosan 5 megfigyelés esik 18 és 19 közé.
    9. Vélhetően ennek a sokasági eloszlásnak erősen pozitív a ferdeség értéke.

A keresett sokaságok rendre: B, D, E, B, C, C, B, D, D.

  1. Számítsa ki a hallgatok.xlsx fájl adatai alapján, hogy
    1. a hallgatók "legokosabb" 10%-a legalább mekkora ösztöndíjjal rendelkezik?
    2. mekkora az a szórakozásra költött összeg, melynél a hallgatók 60%-a többet, 40%-a kevesebbet költ?

  1. A sokasági eloszlás 90. percentilisét keressük. A következő függvény alkalmazható: =PERCENTILIS.TARTALMAZ(sokaság; 0,9). Tehát \(24\,000\) forint, vagy annál magasabb ösztöndíjjal rendelkeznek.

  2. A 40. percentilist keressük. A következő függvény alkalmazható: =PERCENTILIS.TARTALMAZ(sokaság; 0,4). Ez az összeg \(2\,000\) forint.

  1. Adott az alábbi osztályközös gyakorisági sor, amely egy településen a vállalatok számát mutatja foglalkoztatotti létszámkategóriánként.
    1. Számítsa ki a relatív gyakoriság, kumulált gyakoriság, értékösszeg, relatív értékösszeg, valamint a kumulált relatív értékösszeget is! Értelmezze a kapott eredményeket!
    2. Mit gondol melyik létszámkategóriában foglalkoztatják a legtöbb embert? Melyik mutatóból tudunk erre következtetni?
foglalkoztatottak száma vállalatok száma (gyakoriság)
-50 200
51-100 50
101-150 40
151-200 50
201- 10
  1. A kapott értékek:
osztályközök \(X^{\ast}_j\) \(F_j\) \(G_j\) \(F_j^{\prime}\) \(S_j\) \(Z_j\) \(Z_j^{\prime}\)
-50 25 200 0,571 200 5000 0,202 0,202
51-100 75 50 0,143 250 3750 0,152 0,354
101-150 125 40 0,114 290 5000 0,202 0,556
151-200 175 50 0,143 340 8750 0,354 0,909
201-250 225 10 0,029 350 2250 0,091 1,000
összesen - 350 1 - 24750 1 -
  1. A 151-200 fős vállalatok foglalkoztatják a legtöbb embert, az értékösszeg (\(S_j\)) alapján.
  1. Az ettermek.xlsx fájl egy kétszemélyes vacsora árait tartalmazza 50 belvárosi és külvárosi étteremre vonatkozóan.
    1. Számítsa ki az alsó és a felső kvartilis értékét és értelmezze is őket!
    2. Mekkora az az ételár, aminél az éttermek 20%-ában drágább a kétszemélyes vacsora?
    3. Készítsen hisztogramot az ételárakról mind a belvárosi, mind a külvárosi éttermek esetén!
    4. Jellemezze a fentiek és egyéb mutatók szerint az ételárak eloszlásait a két helyszínen!
  1. Alsó kvartilis: =KVARTILIS.TARTALMAZ(sokaság;1) 36,75€ az az ár, aminél az éttermek negyede olcsóbb, háromnegyede pedig drágább. Felső kvartilis: =KVARTILIS.TARTALMAZ(sokaság;3) 53,25€ az az ár, aminél az éttermek negyede drágább, háromnegyede pedig olcsóbb.
  2. A negyedik kvintilist, azaz a 80. percentilis értékét keressük. =PERCENTILIS.TARTALMAZ(sokaság; 0,8) Az érték 56€.
  3. A hisztogramok elkészítéséhez alkalmazzunk szűrőt először a belvárosi, majd a külvárosi éttermekre. Ezután az egyes kategóriákra készíthetünk hisztogramot.
  4. A jellemzéshez használhatjuk a következő mutatókat: csúcsosság, ferdeség, átlag, medián, interkvartilis terjedelem
  1. Nyissa meg a TOP100.xlsx fájlt!
    1. Számítsa ki a boxplot rajzolásához szükséges mutatókat az árbevétel változó használatával!
    2. Készítsen hisztogramot az árbevétel változó alapján, ügyeljen a "kerek" osztályközhatárokra!
    3. Számítsa ki és értelmezze a csúcsosság, ferdeség mutatókat!
    4. Jellemezze a változó eloszlását a fenti mutatók alapján!
  1. A feladat megoldásához a KVARTILIS.TARTALMAZ függvény használata javasolt:
mutató érték függvény
MIN 86437 =KVARTILIS.TARTALMAZ(árbevétel;0)
Q1 119413,75 =KVARTILIS.TARTALMAZ(árbevétel;1)
Q2 = Me 172968,5 =KVARTILIS.TARTALMAZ(árbevétel;2)
Q3 280375 =KVARTILIS.TARTALMAZ(árbevétel;3)
MAX 5343234 =KVARTILIS.TARTALMAZ(árbevétel;4)

Ezek alapján az alábbi boxplot szerkeszthető:

A legújabb Microsoft Office csomagban található Dobozdiagram (Beszúrás menü, Diagramok almenü, Statisztikai diagramok rész) segítségével is könnyedén szerkeszthető boxplot ábra:

Az ábráról leolvasható, hogy az adatállomány árbevétel változója több kiugró értéket (outlier) is tartalmaz, ezek közül a Mol Nyrt egyfajta extrém kiugró értékként viselkedik (a z-értéke \(8,9325\), ami lényegesen nagyobb, mint \(3\)). Ezt az értéket elhagyva egy "szebb", informatívabb ábrát kapunk (több dolgot is könnyebben le tudunk olvasni):

Meg kell jegyezzük azonban, hogy a Mol Nyrt elhagyásával meg fog változni az átlag és a szórás értéke is, ezáltal az ezen értékek által számított z-score értékek is, ami azt is eredményezi, hogy míg korábban (a Mol Nyrt-vel) "csupán" 1 darab extrém kiugró értékünk volt, úgy a Mol Nyrt elhagyását követően ezek száma 2 darab lett. A kiugró értékek (helyes) kezelésének bőséges irodalma van, ez nem képezi jelen tananyag részét.

  1. A "kerek" osztályközhatárok megállapításához használhatjuk a tankönyvben található képleteket is, de az esetek többségében a legcélszerűbb szemrevételezés útján megfelelő osztályközhatárt meghatározni. Egy lehetséges megoldás a 100000 lehet. Az így kapott hisztogram a következő:

Ahogy azt az előző feladatrészben megállapítottuk, az árbevétel változóban több kiugró érték is szerepel (ezek a hisztogramon is jól kivehetőek), a Mol Nyrt egyfajta extrém értékként viselkedik, ezt elhagyva egy "szebb" ábrát kapunk:

mutató érték Excel függvény
K 64,415 =CSÚCSOSSÁG(árbevétel)
S 7,343 =FERDESÉG.P(árbevétel)
  1. Az árbevétel változó ferdeségének értéke 7,343, ami egy jobboldali (pozitív) ferdeséget jelent. Ha a változó mediánját (172968,5) összehasonlítjuk az átlagával (310311), akkor ugyancsak ezt tapasztalhatjuk, hiszen az átlag értéke meghaladja a medián értékét. A csúcsosság szempontjából elmondható, hogy ezen mutató értéke 64,415, ami egy erősen pozitív szám, így (a normálishoz képest) egy csúcsos eloszlásról beszélhetünk. Ezt a megállapításunkat erősíti az interkvartilis terjedelem is, hiszen az adatok 50%-a egy igen keskeny sávba esik. Ugyanakkor a változó több kiugró értéket tartalmaz, amelyek közül a MOL Nyrt extrém kiugró érték, azonban ezt figyelmen kívül hagyva is hasonló eredményeket kapunk.
  1. Nyissa meg a lakasok.xlsx fájlt és vizsgálja meg az ár változót a lakások munkalapon!
    1. Jellemezze a panel lakásokat árait az ún. five-number summary értékkel és számolja ki a változó átlagát. Mit tud elmondani az eloszlás alakjáról?
    2. Számítsa ki a panel lakásokra vonatkozó megfigyelések csúcsosságát és ferdeségét! Ezek alapján milyen a változó eloszlása?
    3. Végezze el az a. és a b. feladat számításait a tégla építésű lakásokra is. Mit tud mondani ebben az esetben az eloszlásról?
    4. Készítsen boxplot ábrát, amin külön a panel és külön a tégla építésű lakások eloszlási jellemzői is láthatók. Írja le, hogy milyen különbségeket és hasonlóságokat talál a panel és a tégla lakások árainak eloszlását tekintve!
mutató érték
\(\text{Min}\) \(33{,}7\)
\(Q_1\) \(42{,}1\)
\(\text{Me} = Q_2\) \(47{,}7\)
\(Q_3\) \(57{,}56\)
\(\text{Max}\) \(99{,}45\)
\(\mu\) \(51\)
mutató érték
Ferdeség \(1{,}58\)
Csúcsosság \(3{,}59\)
  1. A tégla lakások esetén a mutatók értékei
mutató érték
\(\text{Min}\) \(41{,}4\)
\(Q_1\) \(60{,}44\)
\(\text{Me} = Q_2\) \(69{,}3\)
\(Q_3\) \(72{,}72\)
\(\text{Max}\) \(109{,}35\)
\(\mu\) \(67\)
Ferdeség \(0{,}44\)
Csúcsosság \(1{,}11\)
  1. A boxplot diagram elemzése több módon történhet, egy lehetséges megoldás az alábbi:

A téglából épült lakások átlagos ára magasabb, mint a panelból épült lakások átlagos ára. A téglalakások esetén 2 darab kiugró érték figyelhető meg, míg a paneloknál 1 darab. A téglalakások árát baloldali (negatív) aszimmetria jellemzi, azaz a téglalakások többségének az ára átlagon felüli. Ezzel szemben a panelok esetén jobboldali (pozitív) aszimmetria figyelhető meg, azaz a panellakások többségének az ára az átlagos ár alatt helyezkedik el. A téglalakások árának interkvartilis terjedelme a panellakások árának interkvartilis terjedelméhez képest keskenyebb, azaz a téglalakások árának eloszlása csúcsosabb, mint a panellakásoké.

  1. Nyissa meg a hasznalt_autok.xlsx fájlt!
    1. Adja meg a használt autók árának interkvartilis terjedelmét!
    2. Készítsen boxplot diagramot! Milyen következtetések vonhatók le az árak eloszlására diagram alapján?
    3. Számítsa ki azt a mutatót, amellyel igazolható a fenti eloszlásra vonatkozó következtetése!
    4. Készítsen osztályközös gyakorisági sort 5 osztályköz létrehozásával az autók korára vonatkozóan, amelyben az első osztályköz felső korlátja 35 legyen, a további osztályközök hossza szintén 35. Mely osztályközben szerepel a legtöbb használt autó? Ez hány százalékát teszi ki az összes használt autónak?
    5. Készítsen hisztogramot a létrehozott gyakoriság tábla segítségével az autók életkorára vonatkozóan! Vizsgálja meg a kapott hisztogramot csúcsosság és ferdeség szempontjából, valamint számítsa ki a mutatókat is!
    6. Hány 4 és hány 5 ajtós autó található az adatbázisban? Készítsen boxplotot mindkét típus áráról! Hasonlítsa össze őket IQR, átlag, medián és terjedelem alapján! Melyik tartalmaz több kiugró értéket?

  1. 811000 vagy 835000

  2. Az átlag a medián felett helyezkedik el, ami jobboldali aszimmetriára enged következtetni. A felső kvartilis és a maximum érték között sokkal nagyobb a távolság, mint a minimum érték és az alsó kvartilis között, ebből is a jobboldali aszimmetria, pozitív ferdeség következik.

  1. Ferdeség: \(1{,}479954811\)

  2. A 106-tól 140 hónapos korig található a legtöbb használt autó az adatállományban. Ez az összes autó \(29{,}52\%\)-a.

alsó felső gyakoriság kumulált gyakoriság relatív gyakoriság
0 35 8 8 \(7{,}62\%\)
36 70 29 37 \(27{,}62\%\)
71 105 28 65 \(26{,}67\%\)
106 140 31 96 \(29{,}52\%\)
141 - 9 105 \(8{,}57\%\)
  1. Az autók korára vonatkozóan közel szimmetrikus hisztogramot látunk, a ferdeség mutató enyhén negatív. Az eloszlás (közepe) lapos, ez a hisztogramról is leolvasható, valamint a negatív csúcsosság mutató is igazolja.

f) A 4 ajtós autók száma 23, míg az 5 ajtósoké 82. Az 5 ajtós autók terjedelme és interkvartilis terjedelme is nagyobb. Az átlag és a medián is magasabban helyezkedik el az 5 ajtós esetben. Az 5 ajtós több kiugró értéket tartalmaz. Mindkét boxplot alapján jobboldali aszimmetriára, pozitív ferdeségre számíthatunk.

  1. Egészítse ki az alábbi táblázatot, majd számítsa ki a kumulált relatív gyakoriságot, és a kumulált relatív értékösszeget! Ábrázolja őket Lorenz-görbe segítségével!
osztályközök \(F_j\) \(F_j^\prime\)
-2000 5
2001-4000 12
4001-6000 52
6001-8000 107
32
10001-12000 11
összesen

A megoldás során használt kerekítések miatt kis mértékben eltérő eredmények születhetnek.

osztályközök \(X^{\ast}_j\) \(F_j\) \(F_j^{\prime}\) \(G_j\) \(\mathbf{G_j^{\prime}}\) \(S_j\) \(S_j^{\prime}\) \(Z_j\) \(\mathbf{Z_j^{\prime}}\)
-2000 1000 5 5 0,0333 0,0333 5000 5000 0,005 0,005
2001-4000 3000 12 17 0,08 0,1133 36000 41000 0 ,0356 0,0406
4001-6000 5000 35 52 0,2333 0,3467 175000 216000 0,1733 0,2139
6001-8000 7000 55 107 0,3667 0,7133 385000 601000 0,3812 0,595
8001-10000 9000 32 139 0,2133 0,9267 288000 889000 0,2851 0,8802
10001-12000 11000 11 150 0,0733 1 121000 1010000 0,1198 1
összesen - 150 - 1 - 10 10000 - 1 -
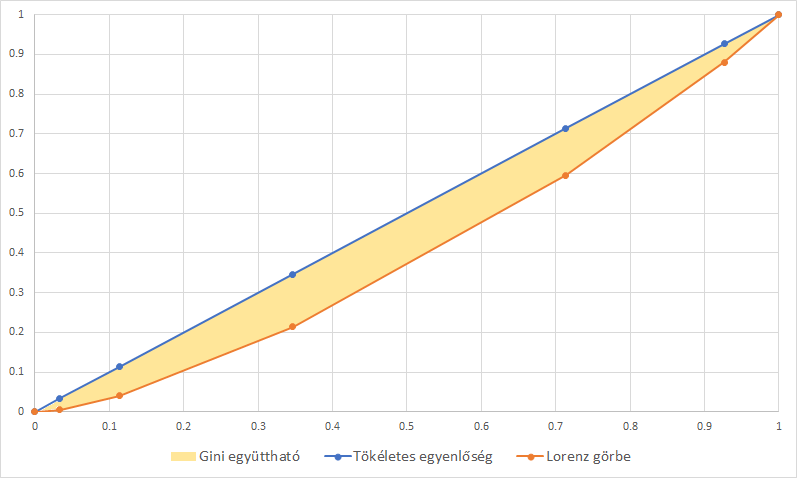
image
image
  1. Nyissa meg a TOP100.xlsx fájlt, majd számítsa ki a \(\gamma_1\) ferdeség mutatót az előadáson tanult képlettel, illetve az Excel FERDESÉG.P függvénnyel az árbevétel változó felhasználásával. Hasonlítsa össze az eredményeket! Mit tapasztal a \(\gamma_2\) mutató esetén?

Az előadáson tanult képlet \(\gamma_1\) ferdeség mutatóra a következő: \[\gamma_1=\dfrac{\frac{1}{N}\sum_{i=1}^{N} (X_i-\mu)^{3}}{\sigma^{3}}\]

Az Excel beépített függvényei segítségével kiszámíthatóak a képletben szereplő ismeretlenek:

mutató érték Excel függvény
\(N\) 100 =DARAB(árbevétel)
\(\mu\) 310311 =ÁTLAG(árbevétel)
\(\sigma\) 563438,2777 =SZÓR.S(árbevétel)

Ezeket behelyettesítve a képletbe az alábbi eredményt kapjuk: \[\gamma_1=\dfrac{\frac{1}{N}\sum_{i=1}^{N} (X_i-\mu)^{3}}{\sigma^{3}} =\dfrac{\frac{1}{100}\sum_{i=1}^{100} (X_i-310311)^{3}}{563438,2777^{3}} =\] \[=\dfrac{\frac{1}{100} \Big[(5343234-310311)^{3}+(1736871-310311)^{3}+\cdots+(86437-310311)^{3}\Big]}{563438,2777^{3}} \approx\] \[\approx 7,343368471\] A FERDESÉG.P függvény használatával az eredmény \(\approx 7,343368471\). A két mutató értéke tehát megegyezik.