4.3 Feltételes valószínűség

Nagyon gyakran arra vagyunk kíváncsiak, hogy egy esemény bekövetkezése befolyásolja-e, és ha igen, milyen mértékben egy másik esemény valószínűségét. Az ehhez hasonló kérdések vizsgálatában a feltételes valószínűség fogalma lesz segítségünkre. Ebben az alfejezetben elsőként definiáljuk a feltételes valószínűséget, majd a definíció segítségével több hasznos tételt, állítást is megfogalmazunk. Az itt megismert fogalmakra épít majd a Statisztikai modellezés tárgy több témaköre is.

Tegyük fel, hogy egy $A$ esemény $\mathbf{P}(A)$ valószínűségét vizsgáljuk, majd tudomásunkra jut, hogy egy $B$ esemény bekövetkezett ($\mathbf{P}(B)\neq 0$). Ennek tükrében az $A$ esemény valószínűsége megváltozhat, ezt a feltételes valószínűséget $\mathbf{P}(A\mid B)$ jelöli, a feltételes eseményt $A$ feltéve $B$, vagy $A$ vonás $B$ eseménynek nevezzük.

Egy új termék bevezetése előtt a vezérigazgató egy adott valószínűséget rendel a termék sikeréhez ($A$). A bevezetés előtti fogyasztói tesztek eredményei ($B$) megváltoztathatják az erről alkotott véleményét mind pozitív, mind negatív irányban.

A sztárbefektető a tőzsdeindex következő negyedévben történő 10%-os emelkedéséhez ($A$) egy adott valószínűséget rendel. A jegybanki alapkamat megváltozása ($B$) ezt a valószínűséget megváltoztathatja, különösen, ha meglepetésként hat.

A társasjáték vége felé közeledve akkor tudok nyerni, ha egy hatoldalú kockával kétszer dobva több mint 10-et dobok ($A$). Az első dobás értéke ($B$) nyilvánvalóan befolyásolja a nyerési esélyeimet.

Ha tehát már tudjuk, hogy $B$ esemény bekövetkezett, akkor a $\Omega$ eseménytér egy -- a $B$-n kívüli -- része már nem következhet be, innentől $B$ válik az eseménytérré. Ez azt jelenti, hogy az eseményteret le kell szűkítenünk. Mivel eddig minden eseményt az eseménytérben található összes elemi esemény számához hasonlítottunk, az új viszonyítási alap $B$ esemény elemi eseményei lesznek. Azt tehát már tudjuk, hogy egy $B$-re feltételes valószínűség nevezőjében $\mathbf{P}(B)$ szerepel. A számlálóban pedig azok az események szerepelnek, ahol $B$ mellett $A$ is bekövetkezik, azaz $\mathbf{P}(A\cap B)$. A gondolatmenet alapján levezetett képlet ténylegesen a feltételes valószínűség definíciója:

$$\begin{equation} \mathbf{P}(A\mid B)=\frac{\mathbf{P}(A\cap B)}{\mathbf{P}(B)} \tag{4.9} \end{equation}$$

azaz az $A$ feltéve $B$ esemény valószínűségét a két esemény együttes bekövetkezési valószínűségének és $B$ valószínűségének hányadosaként definiáljuk, feltéve hogy $\mathbf{P}(B) > 0$. A feltételes valószínűség kiszámításának logikáját mutatja be a 4.2. ábra.

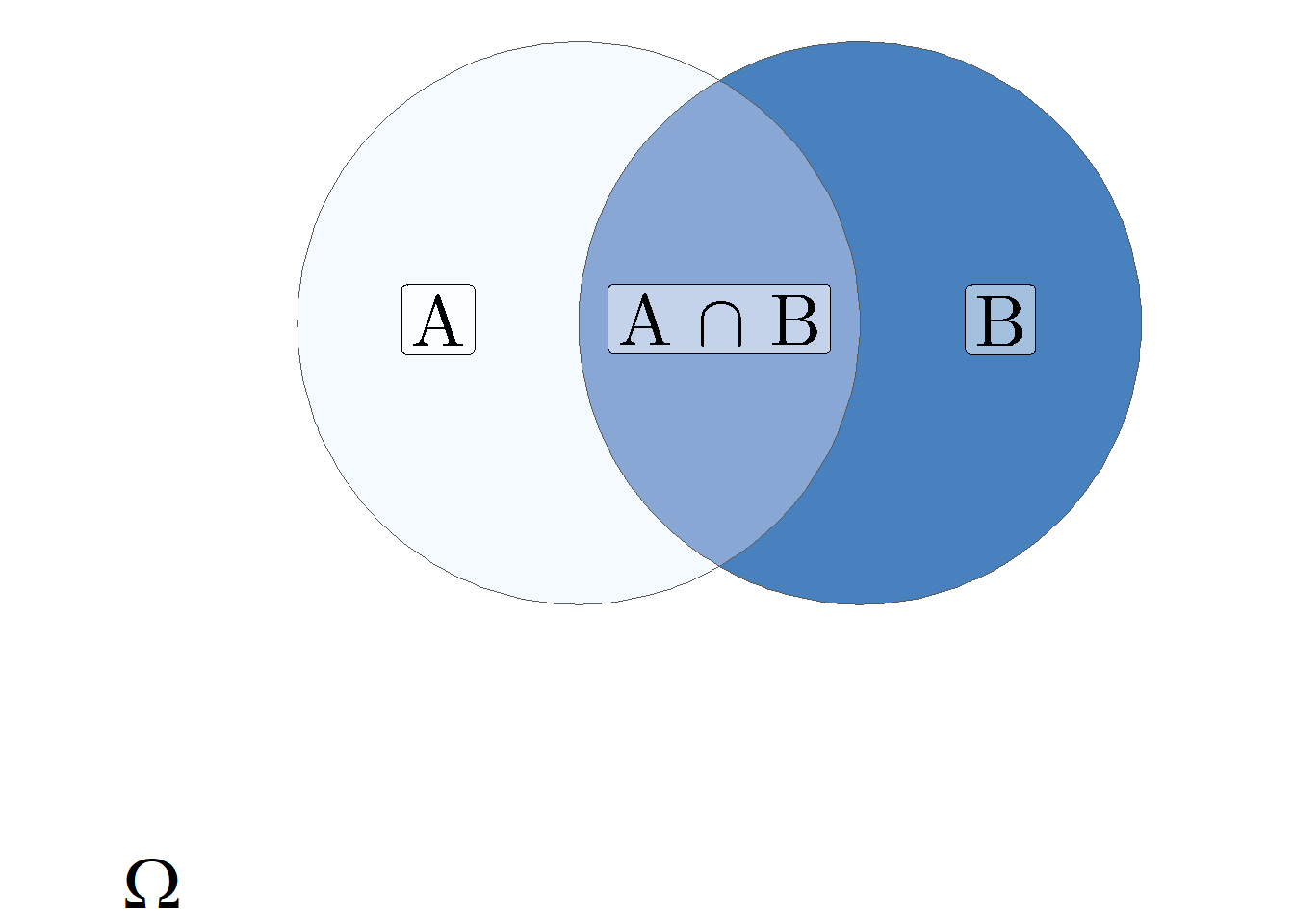
Ábra 4.2: A feltételes valószínűség illusztrációja

A (4.9) definícióból egyben a fordított feltételes valószínűség is adódik (feltételezve, hogy $\mathbf{P}(A)\neq 0$), azaz

$$\begin{equation} \mathbf{P}(B\mid A)=\frac{\mathbf{P}(A\cap B)}{\mathbf{P}(A)} \tag{4.10} \end{equation}$$

hiszen az együttes bekövetkezési valószínűség felcserélhető, $\mathbf{P}(A\cap B)=\mathbf{P}(B\cap A)$.

Folytassuk a fentiek közül a legegyszerűbb példával, legyen tehát

• $A=\{\text{a dobott számok összege több mint 10}\}$,
• $B=\{\text{az első dobás 6-os}\}$.

Ebben az esetben a (4.9) és (4.10) formulák valamennyi elemét egyszerű módszerekkel ki tudjuk számítani, így mintegy "ellenőrizve" a képletek helyességét. Ekkor

• $\mathbf{P}(A)=\frac{3}{36}$, hiszen a $6^2 = 36$ lehetőségből (lásd (4.7)) mindössze 3 sorozat kedvező: $(6,5); (6,6); (5,6)$
• $\mathbf{P}(B)=\frac{1}{6}$, egyszerűen annak a valószínűsége, hogy az első dobás hatos.
• $\mathbf{P}(A\cap B)=\frac{2}{36}$, tehát annak a valószínűségét keressük, hogy nyerünk ÉS elsőre hatost dobunk. Az összes eset száma szintén 36, a kedvező események száma pedig 2: a $(6,5)$ és $(6,6)$ dobás sorozatok.
  
• $\mathbf{P}(A\mid B)=\frac{2}{6}$, hiszen ha már tudjuk, hogy elsőre 6-ost dobtunk, akkor az összes esemény száma 6, ebből pedig két kedvező esemény van, ha 5-öst, vagy ha újra 6-ost dobunk.
• $\mathbf{P}(B\mid A)=\frac{2}{3}$, hiszen ha már tudjuk, hogy tíznél többet dobtunk, akkor az összes esemény száma 3, ebből pedig két kedvező esemény van.

Behelyettesítve tehát $$\mathbf{P}(A\mid B)=\frac{\mathbf{P}(A\cap B)}{\mathbf{P}(B)} = \frac{2}{6}=\frac{\frac{2}{36}}{\frac{1}{6}} \quad \mathbf{P}(B\mid A)=\frac{\mathbf{P}(A\cap B)}{\mathbf{P}(A)} = \frac{2}{3}=\frac{\frac{2}{36}}{\frac{3}{36}}$$

Az esetek nagy részében természetesen nem az a cél, hogy a (4.9) és (4.10) formulák valamennyi elemét kiszámítsuk, ahogy ebben az egyszerű példában történt, hanem pontosan az, hogy általában két tag könnyebben meghatározható, mint a harmadik, mely meghatározásában segítenek a formulák.

Sok esetben épp a (4.9) és (4.10) formulákban szereplő együttes bekövetkezési valószínűségek kiszámítása okoz problémát, azonban ismert valamelyik feltételes valószínűség. Elemi matematikai ismeretek segítségével belátható a valószínűségek szorzási szabálya

$$\begin{equation} \mathbf{P}(A\cap B)=\mathbf{P}(A\mid B)\mathbf{P}(B)=\mathbf{P}(B\mid A)\mathbf{P}(A) \tag{4.11} \end{equation}$$

A szorzási szabály kettőnél több esemény esetére is értelmezhető, ez azonban meghaladja tananyagunk kereteit.

Szintén a feltételes valószínűség definícióján alapul két esemény sztochasztikus függetlensége, az $A$ eseményt a $B$ eseménytől függetlennek nevezzük, ha

$$\begin{equation} \mathbf{P}(A\mid B)=\mathbf{P}(A) \tag{4.12} \end{equation}$$

A definíció logikus, azt mondja ki, hogy ha $B$ bekövetkezése nem változtatja meg $A$ bekövetkezési valószínűségéről alkotott véleményünket, akkor $A$ esemény független $B$-től.

Abban az esetben, ha $A$ és $B$ események nem nulla valószínűségűek, belátható, hogy $A$ függetlensége $B$-től egyben $B$ függetlenségét is jelenti $A$-tól, azaz a tulajdonság szimmetrikus.

Felhasználva (4.11) és (4.12) definíciókat a függetlenség egy másik, gyakran használt definícióját kapjuk. Az $A$ és $B$ eseményeket tehát függetlennek nevezzük, ha

$$\begin{equation} \mathbf{P}(A\cap B)=\mathbf{P}(A)\mathbf{P}(B) \tag{4.13} \end{equation}$$

A (4.13) formulát kimondva, kimondatlanul nagyon gyakran fogjuk használni mind a következő két fejezetben, mind később, a Statisztikai modellezés kurzuson. A függetlenség kettőnél több eseményre is definiálható, jelen tananyagban azonban nem térünk ki erre az esetre.

A teljes valószínűség tétele szintén feltételes valószínűségekre vonatkozó összefüggés. A korábbiakban ((4.1) és (4.2)) már definiáltuk a teljes eseményrendszer fogalmát. A teljes valószínűség tétele azt mondja, hogy ha $A_1, A_2, \dots, A_n$ események teljes eseményrendszert alkotnak, akkor az eseménytér bármely $B$ eseményének valószínűsége meghatározható a

$$\begin{equation} \mathbf{P}(B)=\sum_{i=1}^n\mathbf{P}(B\mid A_i) \mathbf{P}(A_i) \tag{4.14} \end{equation}$$

módon.

A feltételes valószínűségek egy újabb fontos alkalmazási területe az ún. Bayes-tétel. Tekintsük (4.11) formulát, amiből egyszerű osztással (feltéve, hogy $\mathbf{P}(B) >0$)

$$\begin{equation} \mathbf{P}(A\mid B)=\frac{\mathbf{P}(B\mid A)\mathbf{P}(A)}{\mathbf{P}(B)} \tag{4.15} \end{equation}$$

adódik. A tételben tehát két feltételes valószínűség szerepel. A $\mathbf{P}(A)$ valószínűséget gyakran "a priori", vagy röviden prior, míg a $\mathbf{P}(A\mid B)$ valószínűséget "a posteriori", vagy röviden poszterior valószínűségnek nevezzük, utalva arra, hogy az $A$ esemény eredeti, valamint a $B$ esemény bekövetkezése utáni valószínűségeiről van szó. Gyakran van szükségünk az utóbbi két tétel, azaz (4.14) és (4.15) együttes alkalmazására, hiszen a Bayes-tétel nevezőjében szereplő $\mathbf{P}(B)$ valószínűség gyakran nem ismert közvetlenül. Tegyük fel, hogy a teljes eseményrendszert alkotó események közül $A_k$ poszterior valószínűségére vagyunk kíváncsiak, ekkor a Bayes-tétel egy alternatív formája

$$\begin{equation} \mathbf{P}(A_k\mid B)=\frac{\mathbf{P}(B\mid A_k)\mathbf{P}(A_k)}{\sum_{i=1}^n\mathbf{P}(B\mid A_i) \mathbf{P}(A_i)} \tag{4.16} \end{equation}$$